Hinged Valve Submerged in Water

[Captain1024]

Homework Statement

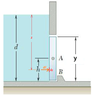
An automatic valve consists of a 225 X 225 mm square plate that is pivoted about a horizontal axis through A located at a distance h = 90 mm above the lower edge. Determine the depth (d) of the water for which the valve will open." Given: h = 90 mm, y = 225 mm
*Answer given in the back of the book = 300 mm*

Diagram: http://imgur.com/BuFIEUU

Homework Equations

F = Pressure(P) * Area(A)

F = ∫∫_A P * dA

Pressure P = ρgh, where
g = 9.81 m/s^2
h = depth in meters
ρ = density = 10^3 kg/m^3

The Attempt at a Solution

My theory: If the force on the valve above the hinge equals the force on the valve below the hinge, the valve will begin to open.

Force on Top: F_TOP = $\int ^{225}_{0}\int ^{225}_{90} \rho g(d-y) dydx$

Simplified: F_TOP = 255$\int ^{225}_{90} \rho g(d-y) dy$

Force on bottom: F_BOT = $\int ^{225}_{0}\int ^{90}_{0} \rho g(d-y) dydx$

Simplified: F_BOT = 255$\int ^{90}_{0} \rho g(d-y) dy$

$\Rightarrow$ F_TOP = F_BOT

Equate: 255$\int ^{225}_{90} \rho g(d-y) dy$ = 255$\int ^{90}_{0} \rho g(d-y) dy$

Simplify: $\int ^{225}_{90} (d-y) dy$ = $\int ^{90}_{0} (d-y) dy$

Integrate: (dy - $\frac{y^2}{2}$|$\stackrel{225}{90}$) = (dy - $\frac{y^2}{2}$|$\stackrel{90}{0}$)

$\Rightarrow$ 135d - 21262.5 = 90d - 4050

$\Rightarrow$ 45d = 17212.5

$\Rightarrow$ d = 382.5 mm

Answer given in book = 300 mm

4. Notes

I know there are many ways to solve this problem. I would like to see a solution involving calculus because I believe that is where all other solution methods are derived from. Thanks in advance.

Captain1024

 

[TSny]

Hello Captain 1024. Welcome to PF!

My theory: If the force on the valve above the hinge equals the force on the valve below the hinge, the valve will begin to open.

You want the hinge to rotate about the axis at A. The rotational analog of force is torque.

 

[Captain1024]

Thank you for your greetings. What equation should I use to find the torque about hinge A?

 

[Chestermiller]

Thank you for your greetings. What equation should I use to find the torque about hinge A?

If p_h is the pressure at the hinge, and z is the distance above the hinge, what is the pressure at z? What is the differential force dF acting on the region of the plate between z and z + dz. What is the moment of this differential force about the hinge? What is the moment about the hinge of all the differential forces for the portion of the plate above the hinge? What is the moment about the hinge of all the differential forces for the portion of the plate below the hinge?

Chet

 

[Captain1024]

P_h = ρ*g*(d-h)

P_z = (d - h - z)(ρg)

Not sure on this part. F = $\int \rho gd*dz$

As for moments, we have been using the sum of the moments about a point are zero to find unknowns. Are you asking me to do the same?

 

[TSny]

Think about filling the container with the fluid. When the depth of the fluid is below point A, you can see that the pressure of the fluid on the plate would create a counterclockwise moment on the plate about point A. The ledge B prevents the plate from opening by exerting a clockwise moment on the plate. As the fluid level rises above point A, the fluid pressure due to fluid above point A will exert a clockwise moment.

The valve will be on the verge of opening when the net torque on the plate (about point A) due to the fluid pressure is zero. So, you need to find the depth d for this situation.

For a strip of the valve of thickness dz at depth z, can you find an expression of the moment arm (relative to A) of the fluid force dF on the strip in terms of d, h, and z?

 

[Chestermiller]

P_h = ρ*g*(d-h)

P_z = (d - h - z)(ρg)

Not sure on this part. F = $\int \rho gd*dz$

No. The differential force is dF = P(z) dz. The differential moment is dM = P(z) zdz. Just integrate the moment over the part of the plate above the hinge. Then integrate the moment over the part of the plate below the hinge.

Chet