- #1
Gregs6799
- 35
- 0
Homework Statement
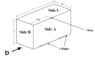
A hinged water storage is shown below. Its top side is denoted as C, the narrow side as B and the long side as A. Assume water density is 1000 kg/m3 and gravity is 9.81 m/s2
Side A is hinged at the bottom edge and secured using a clasp at its top edge.
Dimensions are: L = 1m, H = 0.5m & W = 0.5m
Calculate the size and location of the water thrust force on side A
2. Homework Equations
I = bh^3 / 12
The Attempt at a Solution
[/B]
I've got the correct 1st moment but not the 2nd moment
I submitted this:
2nd moment of area
I = bh^3 / 12
I = 1 x 0.5^3 / 12 = 0.0104
1.00 x 0.5^2 / 12 + 1.00 x 0.5 x 0.25^2 = 0.0520 and been told the formula is wrong but in my notes it says I = bh^3 / 12 is the correct formula.
Any help would be really appreciated.
Greg.
[Moderator: Bold text made plain.]
Last edited by a moderator: