- #1
Paul Gray
- 11
- 0
Hello again :),
I have to solve a rather extensive task. Most important are questions a) and c). I appreciate any help :)!
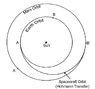
The task: Determine characteristics of a Hohmann transfre towards, when circular planetary orbits around the Sun with [itex]R_E = 149.6 \cdot 10^6 km[/itex] for Earth and [itex]R_M = 227.9 \cdot 10^6 km[/itex] for Mars are used.
The task:
a) How does the true anomaly in [deg] of the Earth's position between start and arrival of the satellite change?
b) What is the angle [deg] between Earth / Sun/ Mars when the satellite arrives at Mars?
c) How many days before opposition (Earth is on a line between Sun and Mars) the launch from Earth must occur to arrive at the apocentre of the transfer ellipse, when Mars is to be encountered.
In different sub-tasks I was already able to identify following.
The orbit transfer time [itex]t_H = 258.8 [days][/itex]
The orbital velocity of Earth [itex]\nu_E = \sqrt{\frac{\mu_{Sun}}{R_E}} = 107224.1113 \frac{km}{h}[/itex]
The orbital velocity of Mars [itex]\nu_M = \sqrt{\frac{\mu_{Sun}}{R_M}} = 86870 \frac{km}{h}[/itex]
The angular velocity of Earth [itex]\omega_E = \frac{360^\circ}{365[days]} = 0.9863\frac{deg}{days}[/itex]
The angular velocity of Mars [itex]\omega_M = \frac{360^\circ}{686.795[days]} = 0.5242\frac{deg}{days}[/itex] (received from the orbital period T).
a) For the true anomaly I only found a formula covering the "One-tangent burn" orbit changing technique: [itex]\nu = \arccos{(\frac{a_{tx}(1-e^2)/r_B-1}{e})}[/itex]. However I do not know, if I can apply this formula to a Hohmann transfer.
b) The satellites travels [itex]180^\circ[/itex] in [itex]258.8 [days][/itex] in the same time. The Earth travels [itex]255.2544^\circ[/itex] and Mars travels [itex]135.6629^\circ[/itex]. Since Mars only performs [itex]135.6629^\circ[/itex] we must have given him a headstart of [itex]44.3371^\circ[/itex]. So the angle at start is [itex]0^\circ[/itex] between Sun and Earth and [itex]44.3371^\circ[/itex] between Sun and Mars. At end the angle between Sun and Earth is [itex]255.2544^\circ[/itex] and [itex]180^\circ[/itex] between Sun and Mars.
Is this correct?
c) From b) I know that Mars needs a headstart of [itex]44.3371^\circ[/itex]. Hence I was able to calculate how many days must have been passed until Mars is in the opposition of earth.
[tex]\omega_E \cdot x = 44.3371 + \omega_M \cdot x \Leftrightarrow x = 94.48 [days][/tex]
After 94.48 days after start Mars opposes Earth. In addition I have no idea how to solve this task :).
Thank you very much for your time!
I have to solve a rather extensive task. Most important are questions a) and c). I appreciate any help :)!
Homework Statement
The task: Determine characteristics of a Hohmann transfre towards, when circular planetary orbits around the Sun with [itex]R_E = 149.6 \cdot 10^6 km[/itex] for Earth and [itex]R_M = 227.9 \cdot 10^6 km[/itex] for Mars are used.
The task:
a) How does the true anomaly in [deg] of the Earth's position between start and arrival of the satellite change?
b) What is the angle [deg] between Earth / Sun/ Mars when the satellite arrives at Mars?
c) How many days before opposition (Earth is on a line between Sun and Mars) the launch from Earth must occur to arrive at the apocentre of the transfer ellipse, when Mars is to be encountered.
Homework Equations
In different sub-tasks I was already able to identify following.
The orbit transfer time [itex]t_H = 258.8 [days][/itex]
The orbital velocity of Earth [itex]\nu_E = \sqrt{\frac{\mu_{Sun}}{R_E}} = 107224.1113 \frac{km}{h}[/itex]
The orbital velocity of Mars [itex]\nu_M = \sqrt{\frac{\mu_{Sun}}{R_M}} = 86870 \frac{km}{h}[/itex]
The angular velocity of Earth [itex]\omega_E = \frac{360^\circ}{365[days]} = 0.9863\frac{deg}{days}[/itex]
The angular velocity of Mars [itex]\omega_M = \frac{360^\circ}{686.795[days]} = 0.5242\frac{deg}{days}[/itex] (received from the orbital period T).
The Attempt at a Solution
a) For the true anomaly I only found a formula covering the "One-tangent burn" orbit changing technique: [itex]\nu = \arccos{(\frac{a_{tx}(1-e^2)/r_B-1}{e})}[/itex]. However I do not know, if I can apply this formula to a Hohmann transfer.
b) The satellites travels [itex]180^\circ[/itex] in [itex]258.8 [days][/itex] in the same time. The Earth travels [itex]255.2544^\circ[/itex] and Mars travels [itex]135.6629^\circ[/itex]. Since Mars only performs [itex]135.6629^\circ[/itex] we must have given him a headstart of [itex]44.3371^\circ[/itex]. So the angle at start is [itex]0^\circ[/itex] between Sun and Earth and [itex]44.3371^\circ[/itex] between Sun and Mars. At end the angle between Sun and Earth is [itex]255.2544^\circ[/itex] and [itex]180^\circ[/itex] between Sun and Mars.
Is this correct?
c) From b) I know that Mars needs a headstart of [itex]44.3371^\circ[/itex]. Hence I was able to calculate how many days must have been passed until Mars is in the opposition of earth.
[tex]\omega_E \cdot x = 44.3371 + \omega_M \cdot x \Leftrightarrow x = 94.48 [days][/tex]
After 94.48 days after start Mars opposes Earth. In addition I have no idea how to solve this task :).
Thank you very much for your time!