- #1
xzbobzx
- 10
- 0
Homework Statement
Alright, this is probably going to be a long one.
For a school project I am trying to simulate (in 2D) our moon's orbit around the earth, to eventually simulate a spaceship doing a hohmann transfer between LEO and LLO whilst being affected by both the Earth's gravity and the moon's gravity.
I am not trying to simulate/solve a three body problem. And the simulation is more of a back of the envelope simulation than a true earth-moon system simulation, but it will serve it's purpose:
The Earth is not affected by the moon.
The moon is only affected by the Earth's gravitational pull and its initial velocity.
The given variables/data/setup:
- I have a coordinate system X and Y, Y goes up, X goes right. The (static) Earth is located at the centre.
- Our moon is located at Y = 385000000 m (the moon's mean orbital distance is 385000 km)
- Moon initial velocity is X = 1023 m/s (the moon's mean orbital velocity is 1.023 km/s)
- Moon mass is irrelevant for now as I'm doing it all based on acceleration, and because the Earth is static.
- Earth mass is 5.97219*10^24 kg.
- A Timestep of 1 second.
Homework Equations
[itex]g = -\frac{GM}{r^2}[/itex]
[itex]g =[/itex] gravitational acceleration
[itex]G =[/itex] gravitational constant
[itex]M =[/itex] Earth mass
[itex]r =[/itex] orbit radius
The Attempt at a Solution
I set up a Microsoft excel project and began coding an macro do to all my heavy lifting:
Code:
Public moon_px As Double 'Position.x (m)
Public moon_py As Double 'Position.y
Public moon_pm As Double 'Position Magnitude
Public moon_vx As Double 'Velocity.x (m/s)
Public moon_vy As Double 'Velocity.y
Public moon_vm As Double 'Velocity Magnitude
Public moon_ax As Double
Public moon_ay As Double
Public moon_am As Double
Public angle As Double 'Angular position relative to earth, 0 = "north", 180 = "south" (degrees)
Public gravity As Double
Public Earth As Double
Public Timestep As Double '(s)
Public Time As Double
Public Iterations As Double
Public i As Double
'---------
Sub TransLunarInjection()
moon_px = Cells(2, 2).Value
moon_py = Cells(3, 2).Value
moon_vx = Cells(4, 2).Value
moon_vy = Cells(5, 2).Value
moon_ax = 0
moon_ay = 0
Time = Cells(6, 2).Value
Timestep = Cells(7, 2).Value
Iterations = Cells(8, 2).Value
i = 1
gravity = 6.67384 * 10 ^ -11
Earth = 5.97219 * 10 ^ 24
moon_vm = Sqr(moon_vx ^ 2 + moon_vy ^ 2)
moon_pm = Sqr(moon_px ^ 2 + moon_py ^ 2)
'moon_ax = 0
'moon_ay = 0
Do While i <= Iterations
Call Moon_Angle(moon_px, moon_py)
moon_vm = Sqr(moon_vx ^ 2 + moon_vy ^ 2)
moon_pm = Sqr(moon_px ^ 2 + moon_py ^ 2)
moon_ax = Sin(angle) * ((gravity * earth) / (moon_pm ^ 2)) * -1 * Timestep
moon_ay = Cos(angle) * ((gravity * earth) / (moon_pm ^ 2)) * -1 * Timestep
moon_vx = moon_vx + moon_ax
moon_vy = moon_vy + moon_ay
moon_px = moon_px + moon_vx
moon_py = moon_py + moon_vy
Cells(i + 1, 4).Value = Time
Cells(i + 1, 5).Value = angle
Cells(i + 1, 6).Value = moon_pm
Cells(i + 1, 7).Value = moon_vm
Cells(i + 1, 8).Value = moon_ax
Cells(i + 1, 9).Value = moon_ay
Cells(i + 1, 10).Value = Sqr(moon_ax ^ 2 + moon_ay ^ 2)
Cells(i + 1, 11).Value = moon_vx
Cells(i + 1, 12).Value = moon_vy
Cells(i + 1, 13).Value = moon_px
Cells(i + 1, 14).Value = moon_py
Time = Time + Timestep
i = i + 1
Loop
End Sub
'---------
Sub Moon_Angle(x As Double, y As Double)
If y > 0 And x = 0 Then angle = 0
If y < 0 And x = 0 Then angle = 180
If x > 0 And y = 0 Then angle = 90
If x < 0 And y = 0 Then angle = 270
If x = 0 And y = 0 Then angle = 0
If y > 0 And x > 0 Then angle = Atn(x / y)
If y < 0 And x > 0 Then angle = 90 + Atn(y / x) * -1
If y < 0 And x < 0 Then angle = 180 + Atn(x / y)
If y < 0 And x > 0 Then angle = 270 + Atn(y / x) * -1
End SubSo what this does, step by step:
1. Calculate the moon's angle relative towards the Earth using simple trigonometry.
2. Calculate the moon's acceleration for both the X and the Y axis, using trigonometry and the gravitational acceleration equation.
3. Apply acceleration to velocity.
4. Apply velocity to position.
5. Print all variables.
6. Advance time by 1 second.
7. Loop.
This doesn't work.
(At first I even planned to do an RK4 implementation but that was a complete nightmare.)
A snippet of my printed values:
Code:
Time = 0s:
Angle = 0°
Distance = 385000000m
Acceleration X = 0m/s^2
Acceleration Y = -0,002688982324817m/s^2
Velocity X = 1023m/s
Velocity Y = -0,002688982324817m/s
Position X = 1023m
Position Y = 384999999,997311m
Time = 3600s: (after one hour)
Angle = 0,00956571126379358°
Distance = 385000184,85925m
Acceleration X = -0,0000257216115406931m/s^2
Acceleration Y = -0,00268885671887548m/s^2
Velocity X = 1022,95368785554m/s
Velocity Y = -9,6828746017381m/s
Position X = 3683767,39436805m
Position Y = 384982561,007074mNow I'm not a rocket scientist, but I do suppose that after one hour, at 1km/s, our moon should have moved along the Y axis a bit more than 17.438km.
After around 7 days the moon should be at Y = 0, at 17.5km/h I doubt it will traverse 385000km
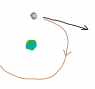
Our X position has moved a lot, however, and extrapolating this we'll see the moon move right indefinitely, whilst only going down a relatively small amount. Like this:
(Black arrow what it is currently doing and brown arrow what it should be doing. I also uploaded it as an attachment for future visitors should this image go down.)
I believe that my calculations are wrong. Or at least the vector implementation of said calculations. (I checked the gravitational acceleration at ground level and it was a steady 9.81m/s^2)
I was wondering if anyone could help me get on track with what I'm doing wrong, or what I should be doing instead. I'm also open to the possibility that my entire idea of how orbital physics should work is off, but if anyone could help me out then that would be greatly appreciated.
Thank you for your time!
Attachments
Last edited: