FallenApple
- 564
- 61
They seem the same to me. So I can have many paths between a and b that are continuously deformable into each other while keeping the endpoints fixed. We say these function form a equivalence class [f]. This should be regardless if the endpoints are the same or not.
The fundamental group seems to be the same situation where the endpoints are the same. So why would they define it as all such [f]. That doesn't make too such sense. If I draw a bunch of lines between a and b, they are all homotopic to each other, and hence we would have one equalvalence class. [f]. How can we have a set? Could it be that there's a set [g] homotopic but not to elements in [f]? Would it be something like a path between a and b but with a self intersecting loop in between?
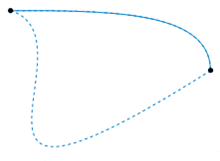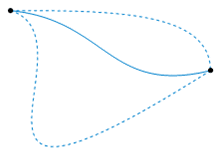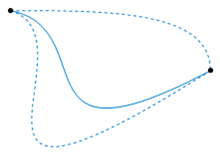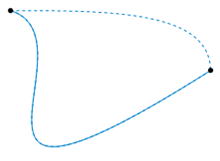
So the following image, source wiki, would it show one such subset of an equivalence class. One with no loops in between? So if I imagine a path inbetween those two points, where there is a self intersecting loop somewhere, then trying to warp it into one of the paths in the image seem like it would tear the curve by contracting an infinite amount of points into a cusp.
The fundamental group seems to be the same situation where the endpoints are the same. So why would they define it as all such [f]. That doesn't make too such sense. If I draw a bunch of lines between a and b, they are all homotopic to each other, and hence we would have one equalvalence class. [f]. How can we have a set? Could it be that there's a set [g] homotopic but not to elements in [f]? Would it be something like a path between a and b but with a self intersecting loop in between?
So the following image, source wiki, would it show one such subset of an equivalence class. One with no loops in between? So if I imagine a path inbetween those two points, where there is a self intersecting loop somewhere, then trying to warp it into one of the paths in the image seem like it would tear the curve by contracting an infinite amount of points into a cusp.
Attachments
Last edited: