Horizon Riddle (Infinite Horizon Problem)

[Whitehole]

I'm reading Cosmology by Harrison and in Chapter 21 he discussed the horizon riddle, I understood the problem that he posed but his solution was confusing.

"Consider two widely separated observers, A (for Albert) and B (for Bertha). We suppose they can see each other. Each has a horizon such that A cannot see things beyond his horizon and B cannot see things beyond her horizon. Each sees things the other cannot see. We ask: Can B communicate to A information that extends A’s knowledge of things beyond his horizon? If so, then a third observer C may communicate to B information that extends her horizon, which can then be communicated to A. Hence, an unlimited sequence of observers B, C, D, E, . . . may extend A’s knowledge of the universe to indefinite limits. According to this argument A has no true horizon. This is the horizon riddle. When we speak of things that are seen or not seen we usually have in mind those that endure (particle horizon) and are represented by world lines.Thus the horizon riddle applies to the particle horizon of the universe. We consider the particle horizon in a static universe (Figure 21.6) and show that the riddle has a simple solution. We have supposed that luminous galaxies originated 10 billion years ago and the particle horizon is therefore at distance
10 billion light years. Observers A and B see each other and have overlapping horizons. Suppose A and B are separated by a distance of 6 billion light years. B sends out information that travels at the speed of light and takes 6 billion years to reach A. Hence A receives from B information that was sent 6 billion years ago when the universe was 4 billion years old. But B’s particle horizon in the past at the time when the information was sent was only 4 billion light years distant. Thus B’s horizon at that time did not extend beyond A’s present horizon. "

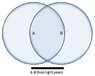
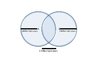
My confusion lies in the statement "Observers A and B see each other and have overlapping horizons. Suppose A and B are separated by a distance of 6 billion light years."

How can A and B be 6 billion light years apart and still see each other given by the time B sent the signal to A the universe was just 4 billion years old. Each observer A and B has a particle horizon 4 billion light years in radius so by overlapping their horizon there is no way that they can have 6 billion light years in separation but still see each other, we are sure that A and B should lie outside of each others particle horizon if their particle horizon have a radius of 4 billion light years, although some of their horizon overlaps.
Also, I don't understand "Thus B’s horizon at that time did not extend beyond A’s present horizon. "

The first image is the confusion. The second image is what I think it should be.

 

[Chronos]

Short of FTL communication, by the time observer B receives the message from A describing events at A's horizon, light from any event observed by A will also have had time to cross the distance from A to B. So, I fail to see how any new information is exchanged.

 

[Whitehole]

Short of FTL communication, by the time observer B receives the message from A describing events at A's horizon, light from any event observed by A will also have had time to cross the distance from A to B. So, I fail to see how any new information is exchanged.

I don't quite understand what you want to point out.

 

[Chronos]

Simply put any signal B can see can also be seen by A by the time a message can travel from B to A. Both the signal and message travel at speed c, so both reach A at the same time.

 

[bapowell]

The universe is expanding?

 

[Whitehole]

The universe is expanding?

Harrison assumed that the universe is static for the sake of his argument.

 

[martinbn]

My confusion lies in the statement "Observers A and B see each other and have overlapping horizons. Suppose A and B are separated by a distance of 6 billion light years."

How can A and B be 6 billion light years apart and still see each other given by the time B sent the signal to A the universe was just 4 billion years old.

I don't see what the problem is here. They are 6 billion years apart and each is 10 billion years old. So, now each sees the other the way he was 6 billion years ago.

Each observer A and B has a particle horizon 4 billion light years in radius so by overlapping their horizon there is no way that they can have 6 billion light years in separation but still see each other, we are sure that A and B should lie outside of each others particle horizon if their particle horizon have a radius of 4 billion light years, although some of their horizon overlaps.

But that was 6 billion years ago. Now their horizons are 10 billion light years and overlap 6. Back then they were only 4 billion light years and didn't overlap.

 

[Whitehole]

I don't see what the problem is here. They are 6 billion years apart and each is 10 billion years old. So, now each sees the other the way he was 6 billion years ago.
But that was 6 billion years ago. Now their horizons are 10 billion light years and overlap 6. Back then they were only 4 billion light years and didn't overlap.

Based on how I understood what he said, they are already overlapping when their particle horizons what still 4 billion light years in radius. That is why I'm confused. But maybe how I understood it was wrong. Should the sentence be structured this way?

"We have supposed that luminous galaxies originated 10 billion years ago and the particle horizon is therefore at distance 10 billion light years. Observers A and B see each other and have overlapping horizons."

THEN

"Suppose A and B are separated by a distance of 6 billion light years. B sends out information that travels at the speed of light and takes 6 billion years to reach A. Hence A receives from B information that was sent 6 billion years ago when the universe was 4 billion years old. But B’s particle horizon in the past at the time when the information was sent was only 4 billion light years distant. Thus B’s horizon at that time did not extend beyond A’s present horizon. "

AS OPPOSED TO

"We have supposed that luminous galaxies originated 10 billion years ago and the particle horizon is therefore at distance 10 billion light years."

THEN

"Observers A and B see each other and have overlapping horizons. Suppose A and B are separated by a distance of 6 billion light years. B sends out information that travels at the speed of light and takes 6 billion years to reach A. Hence A receives from B information that was sent 6 billion years ago when the universe was 4 billion years old. But B’s particle horizon in the past at the time when the information was sent was only 4 billion light years distant. Thus B’s horizon at that time did not extend beyond A’s present horizon. "

 

[eloheim]

I think I generally agree with Chronos's first reply here: Any information that B could pass along to A could just as well travel straight through empty space (imagining as if B didn't exist at all) and go right on to A at light speed with no difference. I don't see how having some dude sitting there changes anything whatsoever.

 

[Flatland]

Let me try to reword what the OP is asking. For the sake of argument let's suppose the Universe is spatially infinite and we have an infinite number of people that can transmit information in a serial fashion (person A, person B, person C...etc). Suppose person Z transmit information about what he sees at his horizon all the way down the chain of command to person A. But suppose person A's horizon is at person G. How can person A receive information about person Z's horizon when the light from person Z's horizon will never reach person A? Is that what the OP is asking?

 

[bapowell]

Let me try to reword what the OP is asking. For the sake of argument let's suppose the Universe is spatially infinite and we have an infinite number of people that can transmit information in a serial fashion (person A, person B, person C...etc). Suppose person Z transmit information about what he sees at his horizon all the way down the chain of command to person A. But suppose person A's horizon is at person G. How can person A receive information about person Z's horizon when the light from person Z's horizon will never reach person A? Is that what the OP is asking?

He'll receive the information from Z. And at that time his horizon will have grown from G to reach Z.

 

[Whitehole]

Let me try to reword what the OP is asking. For the sake of argument let's suppose the Universe is spatially infinite and we have an infinite number of people that can transmit information in a serial fashion (person A, person B, person C...etc). Suppose person Z transmit information about what he sees at his horizon all the way down the chain of command to person A. But suppose person A's horizon is at person G. How can person A receive information about person Z's horizon when the light from person Z's horizon will never reach person A? Is that what the OP is asking?

In a sense but my confusion really arised from how Harrison constructed his sentences, I completely understand what he wants to point out but his wording kinda gets me confused. That is why I want to clarify what he stated (As I said above).

 

[Flatland]

He'll receive the information from Z. And at that time his horizon will have grown from G to reach Z.

Would the answer still be the same if it's the event horizon rather than the particle horizon?

 

[bapowell]

Would the answer still be the same if it's the event horizon rather than the particle horizon?

No, because if an event horizon separates A and Z they can never exchange light signals.

 

[Flatland]

No, because if an event horizon separates A and Z they can never exchange light signals.

So unlike particle horizons event horizons can't overlap?

 

[bapowell]

So unlike particle horizons event horizons can't overlap?

They can. Event horizons delineate those events that will and those events that will never be observed. If A and Z are outside each other's event horizons (which may overlap) they cannot communicate now or any time into the future.

 

[ebos]

The particles reaching A's eye (let's say they're photons) would probably even reach B before A's report to B because A still needs to receive, process and resend the photons. By that time they'd be well on their way to B, wouldn't they? Just because objects are separated by FTL spacetime expansion don't some of these photons still 'catch up' to, in this case, B?
Also, isn't the word 'horizon' kind of a misnomer since one never really catches up to a horizon so it would be difficult to say that A exists on B's horizon? Please straighten me out where I've screwed up, if I have, because the more I usually wind up thinking about this type of subject, the 'confuseder' i get.

 

[ebos]

Oh, I forgot something... Is it actually possible to have 2 people (in this scenario) to be able to see each other yet still maintain their own separate horizons? Since spacetime is curved and the further A can see the more curved A's horizon becomes and therefore wouldn't A also see everything in B's horizon? For example, if it is possible to one day see back to the BB wouldn't one then not see everything?

 

[bapowell]

Oh, I forgot something... Is it actually possible to have 2 people (in this scenario) to be able to see each other yet still maintain their own separate horizons? Since spacetime is curved and the further A can see the more curved A's horizon becomes and therefore wouldn't A also see everything in B's horizon? For example, if it is possible to one day see back to the BB wouldn't one then not see everything?

Sure. It's possible for you and I to talk but for there to be someone else that you can talk to that I cannot.

 

[ebos]

OK, humour me. Let's just go back to the inflating balloon analogy that Phinds always refers to. Say A and B are opposite ends of the balloon i.e. 100 degrees or so from each other. However, when they first looked at one another the balloon was a lot smaller and they could then see each other peering above each other's horizons (Unless of course they were themselves much tinier and grew as the balloon grew but I don't think that is an issue here.). I know the universe is not a balloon but that analogy works so well in so many other scenarios that I'm stuck with that picture. Tell me it at least kind of makes sense. 'K?

 

[Chronos]

Whatever A can see is causally disconnected from what B sees, but, that is a strictly temporary condition. A cannot communicate his observations to B before that information reaches B independent of any efforts by A.

 

[Flatland]

They can. Event horizons delineate those events that will and those events that will never be observed. If A and Z are outside each other's event horizons (which may overlap) they cannot communicate now or any time into the future.

So it would be impossible for say A and B are within each other's event horizon, B and C are within each other's event horizon, but A and C are not within each other's event horizon?

 

[bapowell]

So it would be impossible for say A and B are within each other's event horizon, B and C are within each other's event horizon, but A and C are not within each other's event horizon?

From what I can tell there are no event horizons in the OP's riddle.

 

[bapowell]

OK, humour me. Let's just go back to the inflating balloon analogy that Phinds always refers to. Say A and B are opposite ends of the balloon i.e. 100 degrees or so from each other. However, when they first looked at one another the balloon was a lot smaller and they could then see each other peering above each other's horizons (Unless of course they were themselves much tinier and grew as the balloon grew but I don't think that is an issue here.). I know the universe is not a balloon but that analogy works so well in so many other scenarios that I'm stuck with that picture. Tell me it at least kind of makes sense. 'K?

The balloon analogy works fine here. What's your question though? Are you asking whether A and B can be in contact if they're on opposite sides of the universe?

 

[ebos]

The balloon analogy works fine here. What's your question though? Are you asking whether A and B can be in contact if they're on opposite sides of the universe?

It's just difficult to think of the universe having opposite sides. 'A' would need some fantastic optics and he would then only see 'B' at the beginning of the universe instead of the opposite end, wouldn't he?

 

[bapowell]

It depends. If A and B are comoving with the expansion (i.e. stationary with respect to the balloon's surface) then they will always see each other on their respective opposite sides. As far as optics are concerned, no need: the photons follow the curvature of the universe just like any other object.

 

[Whitehole]

From what I can tell there are no event horizons in the OP's riddle.

There is no event horizon in this case because the universe is assumed to be infinite and eternal for the sake of what Harrison wants to point out. Basically, my confusion arised from what I stated in my post #8. If what I stated there is correct then Harrison is talking about the present in which A and B can see each other and the age of the universe is 10 billion years so each of their particle horizon is 10 billion light years in radius and overlapping. Now he went to the past to show how everything happened. Suppose A and B is 6 billion light years away (which is the distance that he did not state when the universe is already 10 billion years old; besides the universe is static so A and B are not moving, the distance between them will not change through time), and suppose we were at the time when the universe was 4 billion years old, so their particle horizon is 4 billion light years and overlapping but not in way that they can see each other (only 2 billion light years are overlapping given they are 6 billion light years away and each has a particle horizon of 4 billion light years). Now B sends a signal that will take 6 billion years to reach A, but by then the particle horizon of A already expanded to 10 billion light years and covered already the information B sent to A so as to help expand his horizon.

Now for Harrison's argument. Now since this is the case, during the time when the universe was 4 billion years old, Harrison wants to show if it is possible for B to expand A's horizon. So B tries to "tell" the information to A so as to expand A's horizon, but that information would take time to reach A, by then A's particle horizon already expanded regardless of whether B did or didn't "tell" A the information, so in conclusion B can't help A to expand his horizon. Thus the true horizon is the particle horizon.

This is how I understood it.

 

[golfrmyx]

definition semantics. do not drive yourself crazy.