tejolson
- 8
- 0
I'm trying to figure out how to do a Lissajous Curve in 3d. It has a 2d shape in the real world, so if it's in the real world, then there must be a 3d shape to it.
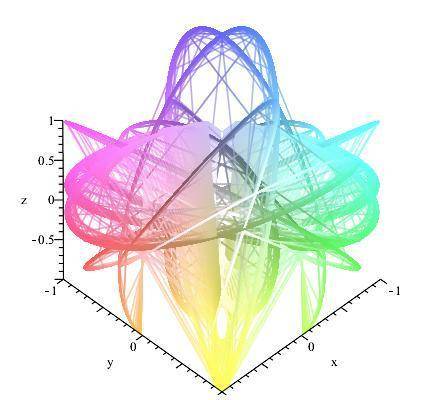
Here is the crazy version, it has 8 variants of the last pic layered and it's at 45 45 0
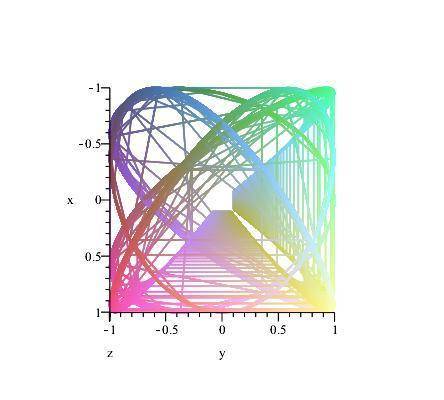
This is the one above and it is at 0 0 0
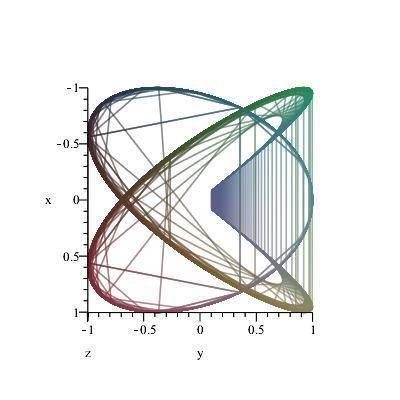
Here is my version of that Lissajous by itself.
There are a million different ways to make pretty shapes out of that curve, but I'm pretty sure there is only one way it can be represented in 3d if it is to represent a real world example.
Here is the crazy version, it has 8 variants of the last pic layered and it's at 45 45 0
This is the one above and it is at 0 0 0
Here is my version of that Lissajous by itself.
There are a million different ways to make pretty shapes out of that curve, but I'm pretty sure there is only one way it can be represented in 3d if it is to represent a real world example.



