- #1
MrKriss
- 7
- 0
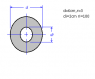
Homework Statement
D1=6cm D2=2cm ( i have to prove that 2nd moment of area (J) of a circulal plate abouts its polax axis(zz) is equal to piD^4/32 )
Homework Equations
The Attempt at a Solution
J=pi6^4/32 - pi2^4/32 = 125.66
J=r1^2x2pirdr
J=Integral 2pir^3d2 = 2pi integral(high 3 , low 1) r^3dr=2pi (r^4/4)(high3 ,low1)
=2pi ((3^4/4)-(1^4/4) = 2pi (20.25 - 0.25) = 2pi x20 = 125.66 (answer is correct ) but i need to show how piD^4/32 is derrived using integration