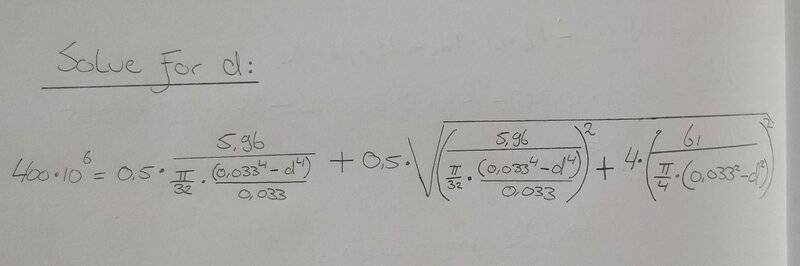How Can I Solve for d in This Equation and What Software Can Verify It?

  • Context: Undergrad 
  • Thread starter Thread starter Mech_LS24
  • Start date Start date
  • Tags Tags
    Approach
Click For Summary
SUMMARY

The discussion focuses on solving a 10th order polynomial equation for the variable "d". Participants recommend using free software tools such as Desmos and Wolfram Alpha for verification. Additionally, they suggest advanced techniques like the Weierstraß substitution and specific variable substitutions (x=0.033² - d² and y=0.033² + d²) to simplify the problem.

PREREQUISITES
  • Understanding of polynomial equations, specifically 10th order polynomials.
  • Familiarity with mathematical substitutions and transformations.
  • Basic knowledge of software tools like Desmos and Wolfram Alpha.
  • Experience with advanced calculus techniques, including Weierstraß substitution.
NEXT STEPS
  • Explore the capabilities of Wolfram Alpha for polynomial equation solving.
  • Learn how to use Desmos for visualizing complex equations.
  • Research the Weierstraß substitution method in detail.
  • Study polynomial factorization techniques for higher-order polynomials.
USEFUL FOR

Mathematicians, students tackling complex polynomial equations, and anyone interested in utilizing software tools for mathematical verification.

Mech_LS24
Messages
148
Reaction score
16
TL;DR
I would like to solve the equation for "d".
Dear mathematicians,

I am getting stuck solving this equation for "d". And what (free)software would you recommend to check this equation?
IMG_20220827_130742__01.jpg


SolveFord.jpg


Thanks a lot!
 
Physics news on Phys.org
Use desmos or something or wolfram alpha
 
Reply
  • Like
Likes   Reactions: topsquark and Mech_LS24
Mech_LS24 said:
Summary: I would like to solve the equation for "d".

Dear mathematicians,

I am getting stuck solving this equation for "d". And what (free)software would you recommend to check this equation?
View attachment 313333

View attachment 313334

Thanks a lot!
Unless something cancels it's going to be a 10th order polynomial. And given your numbers it's highly unlikely to be factorable. W|A, Mathematica, or Matlab would be my suggestions.

-Dan
 
Reply
  • Like
Likes   Reactions: fresh_42 and Mech_LS24
If you really want to attack that expression, I recommend the substitutions ##x=0.033^2 -d^2 ## and ##y=0.033^2+d^2##. And you should consider using a Weierstraß substitution!
 
Reply
  • Like
Likes   Reactions: Mech_LS24, topsquark and malawi_glenn

Similar threads

Undergrad Solving a system of equations with 5 unknowns
  • · Replies 10 ·
Replies
10
Views
1K
Undergrad Numerical Relativity -- Software to solve the Einstein field equations?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Software for entering Mathematics Equations
  • · Replies 5 ·
Replies
5
Views
677
Graduate What is the geometric approach to mathematical research?
  • · Replies 2 ·
Replies
2
Views
1K
Undergrad Solving a System of Nonlinear Equations Symbolically
  • · Replies 9 ·
Replies
9
Views
3K
Engineering Deflection and Slope of a Simply Supported Beam
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad How to Set Up Equations for a Shape with a String Constraint Around a Rectangle?
  • · Replies 20 ·
Replies
20
Views
2K
Undergrad Open source software for integer programming
  • · Replies 3 ·
Replies
3
Views
2K
High School Solving equations but getting an identity - what mistakes were made?
  • · Replies 4 ·
Replies
4
Views
1K
Undergrad How was this substitution possible?
  • · Replies 5 ·
Replies
5
Views
1K