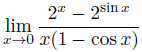SUMMARY
The discussion focuses on solving the limit of the expression \(\frac{2^x - 2^{\sin(x)}}{x(1 - \cos(x))}\) without employing L'Hôpital's rule. The solution utilizes Maclaurin series expansions for \(2^x\), \(2^{\sin(x)}\), and \(\cos(x)\) to derive the limit as \(\frac{1}{3} \ln(2)\). The participant Dan elaborates on the algebraic manipulation required to achieve this result, emphasizing the elegance of the solution despite its complexity.
PREREQUISITES
- Understanding of limits in calculus
- Familiarity with Maclaurin series expansions
- Knowledge of trigonometric functions and their properties
- Basic algebraic manipulation skills
NEXT STEPS
- Study Maclaurin series and their applications in calculus
- Learn about alternative methods for solving limits without L'Hôpital's rule
- Practice solving trigonometric limits using series expansions
- Explore advanced calculus topics related to continuity and differentiability
USEFUL FOR
Students preparing for calculus exams, educators teaching limit concepts, and anyone interested in advanced algebraic techniques for solving limits without L'Hôpital's rule.