Discussion Overview
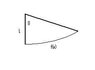
The discussion revolves around the application of the Newton-Raphson method to solve an equation related to a triangle with two straight sides and one curved side defined by an exponential function. Participants explore the challenges of deriving the necessary equations and numerical solutions, particularly in the context of image processing.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses uncertainty about converting the function into polar coordinates and seeks guidance on solving for the unknown side of the triangle.
- Another participant inquires about the nature of the problem, clarifying that it is related to a project rather than homework.
- The application of the problem is identified as image processing, with the participant mentioning difficulties when approaching 90 degrees in their calculations.
- A suggestion is made to write the equation of the straight side in slope-intercept form and to find the intersection with the curved function, using numerical techniques.
- Concerns are raised about the behavior of the equations when theta approaches 90 degrees, with a participant noting that the line becomes horizontal.
- A later reply introduces the need for the Lambert W function when equating the linear function with the exponential function, prompting a request for additional suggestions.
- Another participant outlines the form of the equation to be solved and recommends using the Newton-Raphson method, emphasizing the importance of selecting an appropriate initial trial value for convergence.
- A participant acknowledges the usefulness of the Newton-Raphson method, recalling its application in approximating square roots.
Areas of Agreement / Disagreement
Participants generally agree on the applicability of the Newton-Raphson method for solving the equation, but there are differing views on the challenges posed by the specific conditions of the problem, such as the behavior near 90 degrees and the use of the Lambert W function.
Contextual Notes
Participants mention potential issues with convergence depending on the initial trial value and the specific characteristics of the functions involved, particularly when approaching critical angles.