How can we parameterize the cycloid traced by a rolling circle?

[mathmari]

Hey!

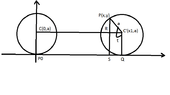
A cycloid is a flat curve that is traced by point of the rim of a circle while the circle rolls without slippage on the line. Show that if the line is the axis $x$ and the circle has radius $a>0$, then the cycloid can be parametrized by $$\gamma (t)=a(t-\sin t, 1-\cos t)$$

Could you give me some hints how we could show that?

 

[MarkFL]

Can you begin by showing the center of the circle $C$ can be given by:

$$C(t)=a\langle t,1 \rangle$$

 

[mathmari]

Can you begin by showing the center of the circle $C$ can be given by:

$$C(t)=a\langle t,1 \rangle$$

Why is the first coordinate equal to $at$ ?

 

[MarkFL]

Why is the first coordinate equal to $at$ ?

Suppose $t$ has increased from $0$ to $2\pi$ so that the circle has rolled one complete revolution. The circle will have moved forward a distance equal to its circumference. :D

 

[mathmari]

Suppose $t$ has increased from $0$ to $2\pi$ so that the circle has rolled one complete revolution. The circle will have moved forward a distance equal to its circumference. :D

So, the distance that the circle has moved forwad is equal to the circumference? Or does this stand only at the case where $t$ has increased from $0$ to $2\pi$ ?

 

[MarkFL]

So, the distance that the circle has moved forwad is equal to the circumference? Or does this stand only at the case where $t$ has increased from $0$ to $2\pi$ ?

Any time $t$ increases by $2\pi$, then the $x$-coordinate of the center of the circle will increase by $2\pi a$. Think of an automobile, where we have marked one of the tires with chalk where it touches the pavement. If the car moves forward, then it will have to move forward a distance equal to the circumference of the tire in order for the mark to return to the pavement.

 

[mathmari]

Any time $t$ increases by $2\pi$, then the $x$-coordinate of the center of the circle will increase by $2\pi a$. Think of an automobile, where we have marked one of the tires with chalk where it touches the pavement. If the car moves forward, then it will have to move forward a distance equal to the circumference of the tire in order for the mark to return to the pavement.

When we have for example that $t$ has increased by an angle, say $r$, it stands that the $x$-coordinate of the center of the circle will be $ra$. Is this correct?

 

[MarkFL]

Yes, this is a result of the arc-length formula for a circular arc:

$$s=r\theta$$

or in our case (if $x$ is the $x$-coordinate of the circle's center):

$$\Delta x=a\Delta t$$

 

[mathmari]

Yes, this is a result of the arc-length formula for a circular arc:

$$s=r\theta$$

or in our case (if $x$ is the $x$-coordinate of the circle's center):

$$\Delta x=a\Delta t$$

Ahaa... Ok... And how could we justify formally that the $x$-coordinate of the circle's center is equal to the arclength?

 

[mathmari]

Is it as follows?

View attachment 4817

Let $P$ a point of the circumference of the circle. We suppose that the point $P$ starts from the point $P_0$, i.e., from the coordinate origin. If the circle rotates by angle $t$, the point that is on the $x$-axis is $Q=(x_1, 0)$ and the point $P$ moves to the position $P(x,y)$. If we unroll the circle we see that $x_1$ is equal to the arc length $PQ$, i.e., $x_1=at$.

We have $$x=P_0S=P_0Q-SQ=x_1-a\cos \left (\phi -\frac{\pi}{2}\right )=a\phi -a\sin \phi =a(\phi -\sin \phi ) \\ y=PS=PR+RS=a\sin \left (\phi -\frac{\pi}{2}\right )+a=-a\cos \phi +a=a(1-\cos \phi )$$

So the cycloid can be parametrized by $$\gamma (t)=a(t-\sin t, 1-\cos t)$$

Is everything correct? Could I improve something at the formulation? (Wondering)

 

[MarkFL]

Looks good to me. :)

 

[mathmari]

Looks good to me. :)

Ok... Thanks a lot! (Mmm)