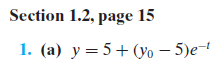How Do Boundary Conditions Affect Differential Equations?
- Context: MHB
- Thread starter karush
- Start date
Click For Summary
SUMMARY
The discussion focuses on solving the first-order linear differential equation $\frac{dy}{dt}=2y-5$ with the initial condition $y(0)=y_0$. Participants clarify the integration process and boundary conditions, leading to the solution $y=\left(y_0-\frac{5}{2}\right)e^{2t}+\frac{5}{2}$. The importance of correctly applying boundary conditions to determine arbitrary constants, such as $c_1$, is emphasized, showcasing the necessity of verifying solutions against the original differential equation.
PREREQUISITES- Understanding of first-order linear differential equations
- Knowledge of integration techniques, particularly with exponential functions
- Familiarity with boundary conditions and their role in determining constants in solutions
- Ability to verify solutions against original equations
- Study the method of integrating factors for solving linear differential equations
- Learn about the role of boundary conditions in differential equations
- Explore the concept of arbitrary constants in differential equations
- Practice solving various first-order differential equations with different initial conditions
Mathematics students, educators, and anyone involved in solving differential equations, particularly those interested in understanding the impact of boundary conditions on solutions.
Similar threads
- · Replies 5 ·
- · Replies 7 ·
- · Replies 6 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 4 ·
- · Replies 9 ·
- · Replies 3 ·