How Do Coupled Pendulums Behave When Connected by a Spring?

[ggilvar99]

Homework Statement

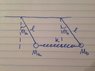
Consider 2 pendulums with the same length L, but 2 different masses Ma and Mb. They are coupled by a spring of spring constant k which is attached to the bobs (the masses).

a) find the equations of motion

b) find the frequencies and configurations of the normal modes

Homework Equations

θ''(t) = -(g/L)sinθ ≈ -(g/L)θ (using small angle approximation to keep the differential equation linear)

The Attempt at a Solution

a) I came up with:
θa''(t) = -(g/L)θa - (k/Ma)(θa - θb)

θb''(t) = -(g/L)θb - (k/Mb)(θb - θa)

b) I tried using θa(t) = θAcos(ωt - ø) and θb(t) = θBcos(ωt - ø) to solve the differential equation but I could not obtain a symmetrical matrix since the masses of the bobs are different.

 

[Simon Bridge]

If you have the period of the pendulums depending on the mass you are doing it wrong.
The coupling would depend on the masses because of the way springs work.

In the static case - there would be an equilibrium separation of the bobs.
The normal modes would oscillate, symmetric and anti-symmetric, about this equilibrium position.
In the symmetric mode, the spring remains at it's equilibrium length - it would be physically equivalent to having the bobs joined by a (massless) rigid rod.

I suspect you have implicitly put the un-stretched length of the spring equal to the separation of the pendulum pivots. I don't see an explicit handling of this, but that would make the symmetric mode equivalent to not having a spring at all.

In normal mode operation, I think, the spring will remain horizontal, but in general it won't.
Though that may not matter with the small-angle approximation - I suspect your success here will depend on how you handle the shift between the linear spring and the circular-motion pendulum bobs.

I think that is where you need to take a closer look.

I don't see any working or reasoning going on there so I don't think I can help further.

 

[ggilvar99]

Thank you for the response. For one of the normal modes I came up with what you were explaining, which is that the spring remains at its equilibrium length, or, in other words, θa = θb. This makes sense with the equations I came up with in part (a) because (k/Ma)(θa - θb) becomes zero, leaving the frequency to be √(g/L).

I did not think to state it explicitly, but yes, I was implying that the spring is at its relaxed length when each pendulum is hanging straight down.

The other normal mode I tried to prove (but failed) was one in which θa = -θb, in which case, as you pointed out, the spring would once again remain horizontal.


I came up with my equations by combining the pendulum motion equation, θ'' = -(g/L)θ, with the equation of motion for masses connected by a spring, x1'' = -(k/m)(x1 - x2). Since in this specific case, x(t) = Lsinθ ≈ Lθ, then θ1'' = -(k/m)(θ1 - θ2), and they combine to get
θ1'' = -(g/L)θ1 - (k/m)(θ1 - θ2). How should I have done this differently to eliminate the dependence on mass?

 

[haruspex]

If you have the period of the pendulums depending on the mass you are doing it wrong.

I don't see why that follows. If you take away the pendulums the period will depend on the masses.

ggilvar99, have you tried finding the eigenvectors?

 

[ggilvar99]

haruspex, I have attempted to find the eigenvectors but I haven't been able to narrow the unknown variables down to 2. In each attempt I've been left with thetaA, thetaB, Ma, and Mb. I'm not sure how to determine the eigenvectors with that many unknowns

 

[TSny]

Ma and Mb are not unknowns. They are just parameters of the system; like g, k, and L.

You want to find the normal mode frequencies in terms of these parameters. Also find the ratio θ_B/θ_A for each mode.

When you substitute your proposed solution into your equations of motion, you should end up with two equations that can each be expressed in terms of the amplitude ratio θ_B/θ_A. You will find that the two equations are consistent only for certain values of ω. Each value of ω will correspond to a certain value of θ_B/θ_A.

 

[Simon Bridge]

The following statement seems to have caused some confusion:

If you have the period of the pendulums depending on the mass you are doing it wrong.

... that is the uncoupled pendulums.
The coupling will depend on the mass as I point out in the very next sentence in the same post #2, therefore the motion of the coupled pendulums will have a mass dependence.

I'd have expected that to be important for the antisymetric normal mode - but not for the symmetric one - for reasons pointed out in post #2 and #4. Thus the closer look. Unfortunately I've been a bit busy so havn't been able to check more closely.

[checking]

From:
θa''(t) = -(g/L)θa - (k/Ma)(θa - θb)
θb''(t) = -(g/L)θb - (k/Mb)(θb - θa)

Guessing the symmetric mode has $\theta_a=\theta_b$, then:
The k/M terms vanishes and I get a frequency that does not depend on the mass.

I guess the desire here is to go via the matrixes?