Find the period of small oscillations (Pendulum, springs)

[castrodisastro]

Homework Statement

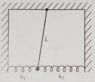
A uniform rod of mass M, and length L swings as a pendulum with two horizontal springs of negligible mass and constants k₁ and k₂ at the bottom end as shown in the figure. Both springs are relaxed when the when the rod is vertical. What is the period T of small oscillations?

Homework Equations

T = 2π/ω
I_{uniform rod} = ⅓ml² = ⅓ML²
ω = √[mgh / I] = √[Mg(½L) / ⅓ML²]

Potential Energy U = mgh = Mg(½L)
Kinetic Energy T = ½kx² = ½(k₁+k₂)L²

The Attempt at a Solution

In order to find the period T, I need to find the angular velocity, ω.

To find the angular velocity I need to know the moment of Inertia for the uniform rod, and we need to know every component that would affect the motion of the rod when disturbed from equilibrium.

The moment of Inertia of the rod is given by ⅓ML²

and the restoring forces are Mg(½L) and ½(k₁+k₂)L²

Solving for T:

= 2π √[(⅓ML²) / (Mg(½L)+½(k₁+k₂)L²]

Factoring out an L from the numerator and denominator, and factoring out a ⅓ from the numerator, and a ½ from the denominator...

= 2π √[((⅓L)ML) / ((½L)(Mg+(k₁+k₂)L))]

The L's cancel and rearranging the ⅓ and the ½ I get...

= 2π √[(2ML)) / (3Mg+3(k₁+k₂)L)]

as my final answer.

The answer in the back of the book however, is

= 2π √[(2ML)) / (3Mg+6(k₁+k₂)L)]

and I have it on good authority that this book is NOT wrong.

Is my reasoning incorrect. Any help is appreciated.

Thank you

 

[TSny]

...the restoring forces are Mg(½L) and ½(k₁+k₂)L²

These expressions don't have the dimensions of force. Are these meant to be restoring torques? Shouldn't the restoring torques depend on the amount of displacement from equilibrium? I don't see anything here that depends on the amount of displacement.

Why do you have a factor of 1/2 in front of the second expression (with the spring constants)?

 

[castrodisastro]

Are these meant to be restoring torques?

Shouldn't the restoring torques depend on the amount of displacement from equilibrium? I don't see anything here that depends on the amount of displacement.

Why do you have a factor of 1/2 in front of the second expression (with the spring constants)?

Yes, I meant restoring torques, my mistake.

From what I read the moment of inertia of a uniform rod is 1/12mr^2. Since it is pivoting about a point that is a displacement L/2 from the center of mass then the moment if inertia becomes 1/3mr^2 via the parallel axis theorem.

And to answer your last question, the factor of 1/2 comes from that being the potential energy of the spring which is 1/2kx^2 and since we have two springs that are not necessarily equal, I took their sum to be equal to k.

Thank you for taking the time

 

[TSny]

Yes, I meant restoring torques, my mistake.

The restoring torques will depend on the position of the rod. For example, when the rod is hanging straight down, the restoring torque is zero. When you wrote your expressions for the restoring torques, at what position of the rod do they apply?

The amount of displacement of the rod from equilibrium may be expressed by the horizontal distance $x$ that bottom of the rod has moved from the equilibrium position. Or, you can specify the amount of displacement of the rod by the angle θ that the rod makes to the vertical. The choice is yours. ($x$ and θ are related in a simple way.) Your restoring torques are going to depend on either $x$ or θ. So, your expressions for the torques should contain either $x$ or θ.

From what I read the moment of inertia of a uniform rod is 1/12mr^2. Since it is pivoting about a point that is a displacement L/2 from the center of mass then the moment if inertia becomes 1/3mr^2 via the parallel axis theorem.

Yes, that is correct.

And to answer your last question, the factor of 1/2 comes from that being the potential energy of the spring which is 1/2kx^2 and since we have two springs that are not necessarily equal, I took their sum to be equal to k.

I was asking about the factor of ½ in your expression ½(k₁ + k₂)L², which you said represents a restoring torque, not a potential energy. So, I'm not quite following your line of thought.

 

[castrodisastro]

The restoring torques will depend on the position of the rod. For example, when the rod is hanging straight down, the restoring torque is zero. When you wrote your expressions for the restoring torques, at what position of the rod do they apply?

The amount of displacement of the rod from equilibrium may be expressed by the horizontal distance $x$ that bottom of the rod has moved from the equilibrium position. Or, you can specify the amount of displacement of the rod by the angle θ that the rod makes to the vertical. The choice is yours. ($x$ and θ are related in a simple way.) Your restoring torques are going to depend on either $x$ or θ. So, your expressions for the torques should contain either $x$ or θ.

Yes, that is correct.

I was asking about the factor of ½ in your expression ½(k₁ + k₂)L², which you said represents a restoring torque, not a potential energy. So, I'm not quite following your line of thought.

Ah I see what you mean...

Since my restoring torques rely on the displacement then if I look at my system when the rod is pointing straight down then there wouldn't be any restoring torques present, but if I choose a different configuration then that means there is some displacement and so I would have to state that displacement.

As for the last question, I thought that the potential energy (the energy that pushes a system towards equilibrium) that the spring is storing is analogous to the torque that is acting on the system to bring it to equilibrium. So my line of thinking is that the angular velocity for objects with moments of inertia is calculated by the square root of (all of the components trying to bring the system back to equilibrium) divided by the moment of inertia of that object.

So to get on the right track, since the question was asking about small oscillations would it be appropriate to choose SATA to be 10 degrees? But now where would a function for theta come in? If I make Mg(1/2L) equal to MgL(1-cos(theta)) it doesn't look correct even though it seems like it tells me the value of torque as the uniform rod rotates away from equilibrium.

Hmmm...

 

[haruspex]

would it be appropriate to choose SATA to be 10 degrees?

I do not know what SATA stands for, but there is no need to choose any specific angle. Just suppose the rod is displaced θ from the vertical. If that angle is small, how far from the centre is the tip? What forces do the springs exert? What torque does gravity produce?

 

[TSny]

Recall that for linear motion of a mass $m$, you get SHM if there is a restoring force proportional to the displacement $x$: $F = -kx$ (Hooke's law)

The period of oscillation is then $T = 2\pi \sqrt{\frac{m}{k}}$

For rotational SHM it is similar. Let $\theta$ be the angle of rotation from equilibrium. Suppose the net restoring torque is proportional to $\theta$ so that

$\tau_{net} = -b \, \theta$ for some constant b.

Then the period of oscillation will be $T = 2\pi \sqrt{\frac{I}{b}}$, where $I$ is the moment of inertia about the pivot.

You already know $I$. So, you just need to find the constant $b$ for your problem. A good free-body diagram will help you set up the correct expressions for the torques.

 

[castrodisastro]

Sorry I was using the Voice to Text feature on my phone and I said "theta" but it heard me as saying SATA.

Ok let me get back to the drawing board and respond to your suggestions tomorrow. Thanks

 

[haruspex]

L(1-cos(theta))

Wouldn't that be the height the end of the rod rises? Why is that interesting?