joshyp93
- 5
- 0
Hello everyone
1. Homework Statement
I have a homework question where I need to find out if the geometry is flat or not. The metric is shown below.
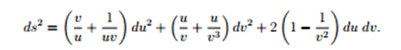
So far I have written the metric in the form guv but and I am trying to find coordinates in which it can be written as the standard Euclidean space matrix ds^2=dx^2+dy^2. I have no idea where to start and cannot seem to find the answer anywhere I look! I just need to know a systematic way of how to check whether it can be expressed as a flat metric or not.
Thanks
Josh
1. Homework Statement
I have a homework question where I need to find out if the geometry is flat or not. The metric is shown below.
Homework Equations
The Attempt at a Solution
So far I have written the metric in the form guv but and I am trying to find coordinates in which it can be written as the standard Euclidean space matrix ds^2=dx^2+dy^2. I have no idea where to start and cannot seem to find the answer anywhere I look! I just need to know a systematic way of how to check whether it can be expressed as a flat metric or not.
Thanks
Josh