Discussion Overview
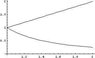
The discussion revolves around finding the area between the curves y=x and y=1/(x^2) bounded by x=2, with particular focus on the challenges posed by the curves not consistently being on top throughout the interval. Participants explore different approaches to defining the area, considering various bounds and intersections.
Discussion Character
- Exploratory
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant suggests that the area should be calculated by integrating the top function minus the bottom function, but expresses confusion due to the curves not being consistently ordered.
- Another participant proposes that the point of intersection might serve as a necessary bound for the area calculation.
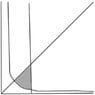
- Several participants discuss the need for a lower boundary, with one suggesting that y=0 could be considered as such.
- One participant outlines a method to treat the area as two separate regions based on the intersection point at (1, 1), detailing the areas to be calculated.
- Another participant questions the clarity of the problem, noting that the area between the curves is not well-defined due to overlapping regions.
- One participant mentions obtaining an area of 1, assuming y=0 is the lower boundary, and expresses uncertainty about this assumption.
- Another participant describes the presence of multiple regions and suggests that the area calculation is complicated by the curves intersecting and overlapping.
- Some participants provide integrals for calculating the area, but there is no consensus on the correct approach or final answer.
- One participant mentions a logarithmic result from integrating, indicating a different perspective on the area calculation.
Areas of Agreement / Disagreement
Participants do not reach a consensus on how to define the area between the curves, with multiple competing views and methods presented. The discussion remains unresolved regarding the correct approach and final answer.
Contextual Notes
There are limitations in the problem definition, particularly regarding the lower boundary and the treatment of overlapping curves. Participants express uncertainty about the assumptions needed for the area calculations.