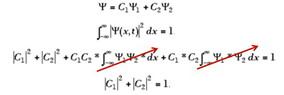How do I normalize a wavefunction with Cn instead of Ci and Cj?
- Thread starter SinaHp
- Start date
Click For Summary
Homework Help Overview
The discussion revolves around normalizing a wavefunction expressed in terms of coefficients Cn, rather than the more traditional Ci and Cj. The context is rooted in quantum mechanics and the properties of wavefunctions within an orthonormal basis.
Discussion Character
- Exploratory, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss taking the inner product of the wavefunction with itself and setting it equal to one. There are mentions of using the Kronecker delta to simplify terms and questions arise about the implications of using different coefficients.
Discussion Status
Participants are actively engaging with the mathematical formulation of the problem, with some providing examples of terms that arise during the normalization process. There is a recognition of the need to express the solution compactly using index notation, indicating a productive direction in the discussion.
Contextual Notes
There are references to the properties of orthonormal bases and the implications of working in complex vector spaces, which may influence the approach to the problem. Some participants express uncertainty about specific steps in the normalization process.
Similar threads
- · Replies 12 ·
- · Replies 11 ·
- · Replies 7 ·
- · Replies 20 ·
- · Replies 1 ·
- · Replies 5 ·