How Do Invariant Hyperbolae Relate to Spacetime Distances?

[snoopies622]

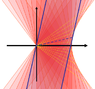
Consider the upper half of the hyperbola

<br /> <br /> (ct)^2 - x^2 = a^2<br /> <br />

where a^2 is a positive constant. The spacetime distance between any point on this curve and the origin is the positive number a. A thought experiment helps give this some physical meaning to me: If I'm at x=0 with a set of identical clocks, and at time = 0 I simultaneously throw them all at different speeds along the x-axis, then the time on every clock when it hits the curve will be the same (a).

Now consider the right half of the hyperbola

<br /> <br /> (ct)^2 - x^2 = b^2<br /> <br />

where b^2 is a negative constant. The spacetime distance between any point on this curve and the origin is also a constant, but I don't know of an analogous thought experiment to help give this hyperbola physical meaning.

Any suggestions?

 

[torquil]

How about thinking of it as the worldline of an object at x = sqrt(-b^2) when t=0, with a constant acceleration in its own rest frame?

Torquil

 

[DrGreg]

How about thinking of it as the worldline of an object at x = sqrt(-b^2) when t=0, with a constant acceleration in its own rest frame?

Torquil

Yes, with a constant proper acceleration of c²/|b|.

 

[snoopies622]

I've seen it derived that the motion of a particle with constant proper acceleration makes that half-hyperbola (thanks to Dr. Greg in an earlier thread) but I don't have an intuitive feel for why a fixed spacetime distance would be the same thing as a fixed proper acceleration.

So I'll have to give it some more thought. Thank you both.

 

[atyy]

The clock measures a timelike length. The rod measures a spacelike length, which is just normal length. I don't know how to make an example as elegant as your clock throwing example, but think along the lines that for observers moving with different constant velocities, one hyperbola is the same temporal separation, while the other is the same spatial separation.

 

[DrGreg]

Imagine lots of rods each of rest-length b and all moving at different speeds longitudinally along the x-axis. They move in such a way that at t=0 all their left-ends are at the origin x=0. In the rest frame of each rod, the right-end of the rod, at that moment, will lie on the hyperbola

c^2t^2 - x^2 = -b^2​

Furthermore, the spacetime envelope of all of the rulers' right ends is that hyperbola. Events to the right of the hyperbola will never be visited by any of the rods, every event on the hyperbola and to its left will be visited by at least one of the rods.

The attached diagram gives the idea. The solid blue lines are the two ends of one of the rods, the dotted blue line joins events that are simultaneous in the rod's rest frame.

______________

Going back to the acceleration example, an observer whose worldline is that hyperbola experiences constant proper acceleration of c²/b, and determines that there is an "apparent horizon" at a distance of b behind her. This horizon behaves pretty much the same as the event horizon of a black hole: nothing, not even light, can cross it towards the observer and something "dropped" by the observer towards the horizon takes an infinite time to reach it according to the accelerating observer.

 

[snoopies622]

Yes, I think those moving rods might be just what I was looking for. I tried to come up with something like that myself this afternoon but - forgetting that simultaneity is relative - couldn't make sense of the fact that only the v=0 rod was horizontal.

Hmm...