How do we show that the interior of a Faraday cage is an equipotential?

[etotheipi]

It is possible to show via Gauss' law that the the net flux through a surface within the Faraday cage must be zero, however this is not a sufficient condition for the electric field to be zero. For the electric field to be zero in the interior of the cage, all points within the cage must be at equal electric potential; I suspect showing this constitutes the other half of the proof.

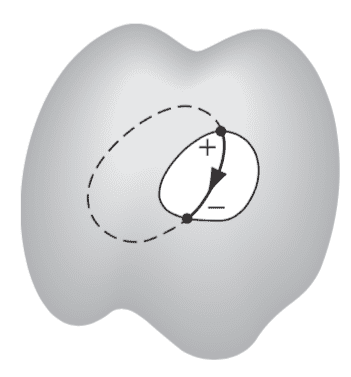
Griffiths proves it another way (please see the diagram below!); if we suppose electric field lines do exist within the cavity, then the voltage change around a closed loop the rest of which is inside the conductor is non-zero, which must be wrong (i.e. KVL). So there can be zero E field in the cavity.

However, I wondered whether it is also possible to prove it the first way through consideration of the potential in the cavity; are there any theorems which might help to do this?

I came across Laplace's equation, which in one dimension $\frac{d^2 V}{dx^2} = 0$ permits a linear potential and consequently a constant electric field, though this doesn't seem to add anything else to the original statement of Gauss' law.

Thank you!

 

[Adesh]

Let’s assume that $\mathbf E$ does exist inside the cavity (when cavity is free from charge). This means that field lines must start at some point on the boundary of cavity and end at some other point on the boundary of the cavity (Griffiths figure) because field cannot exist inside the conductor.

For any Gaussian surface we will have $$\oint \mathbf E \cdot d \mathbf a = 0 \\
\int_V \left (
\nabla \cdot \mathbf E \right) dV = 0 $$
Since, this is true for any volume $V$ therefore we have $\nabla \cdot \mathbf E =0$. This contradicts the fact field lines must come out and sinks down . (Because electric field have zero curl and hence cannot form closed loops). Therefore, electric doesn’t exist inside the cavity.

 

[etotheipi]

For any Gaussian surface we will have $$\oint \mathbf E \cdot d \mathbf a = 0 \\
\int_V \left (
\nabla \cdot \mathbf E \right) dV = 0 $$
Since, this is true for any volume $V$ therefore we have $\nabla \cdot \mathbf E =0$.

But doesn't this just mean the net flux per unit volume is zero? That is, we could still have a uniform electric field within the cavity, with the field lines originating and terminating at points on the cavity boundary, and have $\nabla \cdot \vec{E} = 0$ for a surface within the cavity.

The argument Griffiths proposed about considering a closed loop seems good to me, however I'm not sure if we can derive it just from a statement of Gauss' Law.

 

[Adesh]

But doesn't this just mean the net flux per unit volume is zero? That is, we could still have a uniform electric field within the cavity, with the field lines originating and terminating at points on the cavity boundary, and have ∇⋅→E=0∇⋅E→=0\nabla \cdot \vec{E} = 0 for a surface within the cavity.

But I said it it is true for any surface, when I did the integral I didn’t assume any particular surface.

If we take a point charge at the origin, we would $\nabla \cdot \mathbf E$ equal to zero for every surface except the one which comprises the charge inside it (that is it passes through the origin).

But in our case $\nabla \cdot \mathbf E =0$ for every surface no matter how we draw it and that’s the contraction because electric field lines must begin and end.

I’m always available for any clarification (or for taking up the flaws in the proof).

 

[etotheipi]

Thanks for your reply @Adesh! I think your argument is correct, so long as the possible Gaussian surface can extend into and outside of the conducting material.

For instance, we might imagine a surface which encloses half of the cavity, half of the conductor and a bit of the outside space. Indeed, if an electric field were to exist, the net flux would be non-zero whilst the enclosed charge would be zero and that gives rise to a contradiction.

Thanks for your help!

 

[vanhees71]

Let’s assume that $\mathbf E$ does exist inside the cavity (when cavity is free from charge). This means that field lines must start at some point on the boundary of cavity and end at some other point on the boundary of the cavity (Griffiths figure) because field cannot exist inside the conductor.

For any Gaussian surface we will have $$\oint \mathbf E \cdot d \mathbf a = 0 \\
\int_V \left (
\nabla \cdot \mathbf E \right) dV = 0 $$
Since, this is true for any volume $V$ therefore we have $\nabla \cdot \mathbf E =0$. This contradicts the fact field lines must come out and sinks down . (Because electric field have zero curl and hence cannot form closed loops). Therefore, electric doesn’t exist inside the cavity.

In addition you also know that in the static case $\mathrm{curl} \vec{E}=0$ too. Helmhotz's fundamental theorem of vector calculus thus tells you that $\vec{E}=0$ within the cavity.

 

[Adesh]

@vanhees71 Thank you sir! Your like is an honour and a certificate too for me.

 

[rude man]

For any Gaussian surface we will have $$\oint \mathbf E \cdot d \mathbf a = 0 \\
\int_V \left (
\nabla \cdot \mathbf E \right) dV = 0 $$
Since, this is true for any volume $V$ therefore we have $\nabla \cdot \mathbf E =0$.

If we add $\nabla \times \mathbf E = 0$ we still haven't shown that the E field = 0.

Consider a parallel plate capacitor, plate separation h, charged to V. In the field between the plates.

$\nabla \cdot \mathbf E = \nabla \times \mathbf E = 0$ .
However, E = V/h.
E can be any constant and still satisfy both equations.

 

[Adesh]

If we add $\nabla \times \mathbf E = 0$ we still haven't shown that the E field = 0.

Consider a parallel plate capacitor, plate separation h, charged to V. In the field between the plates.

$\nabla \cdot \mathbf E = \nabla \times \mathbf E = 0$ .
However, E = V/h.
E can be any constant and still satisfy both equations.

If our Gaussian surface contains the plate then we won’t get $\nabla \cdot \vec{E} =0$ But in the case of cavity we would get zero divergence no matter what Gaussian surface we take inside the or comprising the cavity.

 

[rude man]

If our Gaussian surface contains the plate then we won’t get $\nabla \cdot \vec{E} =0$ But in the case of cavity we would get zero divergence no matter what Gaussian surface we take inside the or comprising the cavity.

Yes I think I misinterpreted the application of your equations.

At the border between the plates and the field the divergence is essentially infinite:
$\nabla \cdot \mathbf E = (V/h) \delta(x)$ if the E field is in the x direction.

 

[vanhees71]

If we add $\nabla \times \mathbf E = 0$ we still haven't shown that the E field = 0.

Consider a parallel plate capacitor, plate separation h, charged to V. In the field between the plates.

$\nabla \cdot \mathbf E = \nabla \times \mathbf E = 0$ .
However, E = V/h.
E can be any constant and still satisfy both equations.

For plates of finite extent that's only an approximation.

The homogeneous field is a solution for two inifintely extended parallel plates with an infinite total surface charge on each of its plates. Of course, for such an unphysical idealized situation Helmholtz's theorem doesn't hold anymore since it assumes that the field vanishes at finity.