Rhysmachine
- 2
- 0
Hey all, first post!
Looking to find a deflection equation for a simply supported overhanging beam with two supports and a point- load at the end of the canteliever. I can determine reactions at the supports but i am having trouble finding deflection between the supports.
Any help is appreciated!
the beam in question looks like (a) in the following picture but if we call L/2 a, instead.
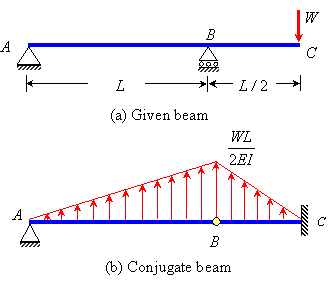
Looking to find a deflection equation for a simply supported overhanging beam with two supports and a point- load at the end of the canteliever. I can determine reactions at the supports but i am having trouble finding deflection between the supports.
Any help is appreciated!
the beam in question looks like (a) in the following picture but if we call L/2 a, instead.