How do you calculate Electric Potential Energy in a Square?

[halo168]

Four identical particles, each having charge q and mass m, are accelerated from rest at the vertices of a square of side L. How fast is each particle moving when their distance from the center of the square doubles?

I used the Conservation of Energy => K_f= -deltaU = U_i-U_f
4(mv^2 /2) = kq^2 (4/L) - kq^2 (4/2L); Solving for v, I would get the wrong answer.

However, the correct answer had 4(mv^2 /2) = kq^2 (4/L + 2/(sqrt(2)*L) - kq^2 (4/2L + 2/(2*sqrt(2)*L)

I know that the (2*kq^2)/(sqrt(2)*L) comes from:

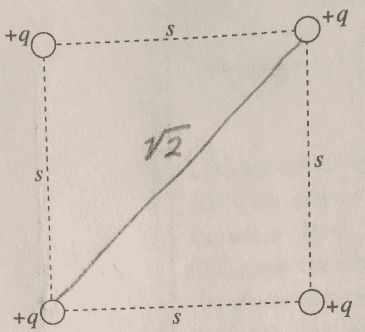
but when I calculate the electric potential energy of three charges (+q) at the vertices of a triangle, I don't need to add an extra term like (2*kq^2)/(sqrt(2)*L ). (Refer to here)

Can someone please explain the difference between calculating electric potential for a square and triangle?

Thanks in advance

 

[TSny]

Hint:
Each pair of charges contributes to the total potential energy.

 

[kuruman]

4(mv^2 /2) = kq^2 (4/L) - kq^2 (4/2L); Solving for v, I would get the wrong answer.

That's because the initial and final potential energy expressions are incorrect. The charges are not equidistant from each other as they are in the video you referred to.