How Do You Calculate the Percentage of People Not Reading Any Newspaper?

[Yankel]

I had a question, but finally cracked it. I apologize for the post.

What I did eventually, I realized that the sum of two events intersections (A and B, A and C , B and C) is equal to 0.18-3*0.08. I then used this sum in the union formula and found my probability.

Hello, I am working on this problem:

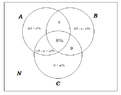
In a country there are 3 newspapers: A,B and C.
39% reads A
36% reads B
30% reads C
18% reads exactly two newspapers
8% read all newspapers
what percentage doesn't read any newspaper ?

What I tried to do, is to sketch a venn diagram with 3 circles, and to figure out how to use the 18% information, but it always looks as if I have too many unknowns. The probability of not reading any newspaper, is the opposite of reading at least one. I tried using the union formula, but it did not work either.

Can you assist please ? Thank you

 

[MarkFL]

Here is a Venn diagram:

View attachment 4983

Add up all the areas and equate them to 100%...what do you find?

 

[MarkFL]

Adding up all the areas (as percentages), we find:

$$(13+y)+(x)+(28-x-y)+(18-x-y)+(8)+(y)+(x+4)+N=100$$

$$13+y+x+28-x-y+18-x-y+8+y+x+4+N=100$$

$$13+28+18+8+4+N=100$$

$$N+71=100$$

$$N=29$$

Thus, we find 29% of the given population read no newspaper.