Vivman
- 2
- 0
- Homework Statement
- The Doppler effect is routinely used to measure the speed of winds in storm systems. As the manager of a weather monitoring sta- tion in the Midwest, you are using a Doppler radar system that has a frequency of 625 MHz to bounce a radar pulse off of the raindrops in a swirling thunderstorm system 50 km away. You measure the reflected radar pulse to be up-shifted in frequency by 325 Hz. Assuming the wind is headed directly toward you, how fast are the winds in the storm system moving?
- Relevant Equations
- Doppler effect equation from Serway: f'(observer frequency) = (c + v)/c * f(source frequency)
Problem Statement: The Doppler effect is routinely used to measure the speed of winds in storm systems. As the manager of a weather monitoring sta- tion in the Midwest, you are using a Doppler radar system that has a frequency of 625 MHz to bounce a radar pulse off of the raindrops in a swirling thunderstorm system 50 km away. You measure the reflected radar pulse to be up-shifted in frequency by 325 Hz. Assuming the wind is headed directly toward you, how fast are the winds in the storm system moving?
Relevant Equations: Doppler effect equation from Serway: f'(observer frequency) = (c + v)/c * f(source frequency)
Attempt at solution was solving for v in the Doppler effect equation. Doing so seems wrong. Is this the correct way of doing it?
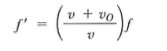

Relevant Equations: Doppler effect equation from Serway: f'(observer frequency) = (c + v)/c * f(source frequency)
Attempt at solution was solving for v in the Doppler effect equation. Doing so seems wrong. Is this the correct way of doing it?