How Do You Determine the Unit Vector in Coulomb's Law?

[laura_a]

Homework Statement

I am a maths teacher retraining in physics, haven't received my textbook yet but attempting the course work, I have the answer to this question and the mathematic skills to solve it, but the notes don't give any worked examples so I have no idea how to go from the law to the answer.

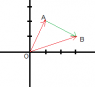
q. A charge q1 is located at x=1 m, y=0. What should you use for the unit vector r in Coulomb's law if you are calculating the force that q1 exerts on charge q2 located at the point x=0 y=1m

Homework Equations

The law I have is F_{12}=[(kq1q2)/r^2]r

The Attempt at a Solution

And I understand the question wants a vector answer and with my maths skills I drew the points and worked out that the distance from q1 to q2 is sqrt(2) and I know the answer is the vector

-sqrt(2)/2 i + sqrt(2)/2 j

Where does the negative come from and why is it over 2? I know this is a silly question but my lecture notes go from the law to this question. I assume the textbook will shed more light but I was just trying to understand this part before moving on.

Thanks to anyone that has time for this :)

 

[Clever-Name]

If q1 is exerting a charge on q2 then what direction is the force acting? Hopefully that will clear up the minus sign troubles.

Also, since r is a UNIT vector it must have a magnitude of one and yet still have the same direction. edit: Keep in mind \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
edit : I should also add that this question doesn't really have anything to do with the law. It is a vector question rather than a force calculation, which would require the use of Coulomb's Law.

 

[laura_a]

Thanks, I realize I have a lot to learn about physics. I realize 1/sqrt(2)=sqrt(2)/2 now that you point it out! But I guess I have no concept of vectors really so I am really in the deep end.

Would it be coincidental that the gradient of the line joining q1 and q2 be negative and the direction gives it a negative sign? Also what are the i and j part of the vector?
I don't even know that part! :(

 

[Clever-Name]

The negative sign is because the arrow is pointing in the negative x direction. I suppose that might be linked with the gradient somehow but I'm too tired to see it at the moment.

A vector can be represented a number of different ways:Simply <x,y> or (x,y) depending on notation is just the location of the tip of the arrow, usually from the origin.

Vectors can also be written as:
x\hat{i} + y\hat{j}

and that means the exact same as my previous notation. i j (and k) represent the unit vectors in the x, y, and z directions respectively.

There are also other ways but hopefully that clears it up.

edit: It might help to write things out explicitly:

\hat{i} = &lt;1, 0, 0&gt;
\hat{j} = &lt;0, 1, 0&gt;
\hat{k} = &lt;0, 0, 1&gt;

Thus x\hat{i} + y\hat{j}
is the same as:
x&lt;1, 0, 0&gt; + y&lt;0, 1, 0&gt;
or
&lt;x, 0, 0&gt; + &lt;0, y, 0&gt;
or
&lt;x, y, 0&gt;

I chose to write it out in 3D coordinates (x,y,z) because usually you deal with all 3 unit vectors i, j and kI mentioned before that usually the vectors are written as though they are starting at the origin. In this case you are explicitly told to find the r vector FROM q1. Thus you can treat q1 as your (origin) when writing out your vector.

 

[cupid.callin]

Any point in 2D (x,y) or 3D (x,y,z) has a vector notation called position vector.

this vector has its head at the point (x,y,z) and tail at (0,0,0)

the other vectors are which are called (not sure) displacement vectors.

they are like ... formed out of 2 position vectors

for points (1,2) and (3,1) position vectors are \vec{OA}, \ \vec{OB}

and vector \vec{AB} \ = \ \vec{OA} \ - \ \vec{OB}

here you have to find a vector something like AB

 

[laura_a]

Thanks heaps, I did learn this at uni (in the 90's) so all has been forgotten! All coming back to me slowly! thanks heaps