How do you find the center axis of a damped oscillation

[sicro]

Hello!

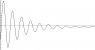
I have data of a damped oscillation (the movement on Y as it dies down in time). Imagine for example a ball that is hanging from a spring and it keeps bouncing up and down under the spring until it stops.

The problem is I do not know how to find the axis around which the oscillation happens.

I need to subtract or add A VALUE to the data I have for the Y points in order to centre the data around an axis -the axis of oscillation-. How do I find out how much to add or subtract?

I tried to find the median of the data points for Y and subtract/add that from the data... It works but it doesn't work well enough. I know that it doesn't work well enough because the curve of decay for the points of the peaks has a slightly different exponent for e than the curve of decay for the troughs (* -1).

PS: I do not have the Y point where the oscillation stops, as the data gathering stopped before a complete stop of the system.

Thank you!

 

[paisiello2]

Why doesn't taking the median work well enough for you? As long as you sum between peak values it should give a reasonable estimate.

 

[sicro]

Because when I create ONE curve by taking the peaks, then get its equation (which is an exponential y=a*(e^(b*x)) ) -using excel- and then ANOTHER by taking the troughs (multiplying by -1 to make it positive), then writing its equation (which is an exponential also)... When I compare the equations of these two curves the value of the exponent for e (b) is different. If I change the median I can get them closer together, but it takes so long to do as each exponent reacts differently to the change of the median value...

:(

 

[paisiello2]

I think I see what you mean.

If you could remove the damping component of the equation and then take the median values, would this give you better results?

 

[AlephZero]

You can eliminate the effect of the offset by taking the difference between successive peaks and troughs and fitting an exponential curve to the differences.

Once you have the decay rate and the frequency, you can then find the peaks and troughs for your decay rate and an amplitude of 1. If you call that list of values $F(t)$, you can match ithe measured data to a curve of the form $a F(t) + b$, and find the best values of a and b by a least squares fit.