mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
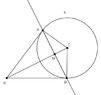
Let $K$ be a circle with center $C=(x_0,y_0)$ and radius $r$. For each point $P=(p_1, p_2)$ outside the circle let $g_P$ be the line that passes through the intersection points of the tangent from $P$ at the circle and the circle.
I want to find the equation of the line $g_p$ (polar).
I have done the following:
Let $A=(a_1, a_2)$ and $B=(b_1, b_2)$ be the two intersection points.
Since $g_p$ passes through these two points the line has the equation of the form:
$$g_P : y=\frac{b_2-a_2}{b_1-a_1}(x-a_1)+a_2$$
The points $A,B$ are on the circle, so we have the following two relations:
$$(a_1-x_0)^2+(a_2-y_0)^2=r^2 \\ (b_1-x_0)^2+(b_2-y_0)^2=r^2$$
We also have that the triangle MBP and AMP are both right triangles so we could use the Pythagorian Theorem, or not? (Wondering)
Or do we have to find the equation of the tangent? (Wondering)
Let $K$ be a circle with center $C=(x_0,y_0)$ and radius $r$. For each point $P=(p_1, p_2)$ outside the circle let $g_P$ be the line that passes through the intersection points of the tangent from $P$ at the circle and the circle.
I want to find the equation of the line $g_p$ (polar).
I have done the following:
Let $A=(a_1, a_2)$ and $B=(b_1, b_2)$ be the two intersection points.
Since $g_p$ passes through these two points the line has the equation of the form:
$$g_P : y=\frac{b_2-a_2}{b_1-a_1}(x-a_1)+a_2$$
The points $A,B$ are on the circle, so we have the following two relations:
$$(a_1-x_0)^2+(a_2-y_0)^2=r^2 \\ (b_1-x_0)^2+(b_2-y_0)^2=r^2$$
We also have that the triangle MBP and AMP are both right triangles so we could use the Pythagorian Theorem, or not? (Wondering)
Or do we have to find the equation of the tangent? (Wondering)