How Do You Integrate y^3 Over a Triangle with Given Vertices?

  • Context: MHB 
  • Thread starter Thread starter ineedhelpnow
  • Start date Start date
  • Tags Tags
    Integrating Triangle
Click For Summary
SUMMARY

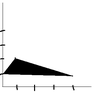
The discussion focuses on calculating the double integral $\iint_D y^3 dA$ over a triangular region defined by the vertices (0,1), (1,2), and (4,1). The correct approach involves determining the limits of integration for both $x$ and $y$. The integral is expressed as $\int_1^2 y^3 (8 - 4y) dy$, where the range for $x$ is derived from the equations of the triangle's sides, specifically $y = x + 1$ for side AB and $x = 7 - 3y$ for side BC. Participants clarify the need for accurate limits and the formulation of the integral.

PREREQUISITES
  • Understanding of double integrals in calculus
  • Familiarity with triangular regions and their equations
  • Knowledge of integration techniques for polynomial functions
  • Ability to derive equations of lines from given points
NEXT STEPS
  • Study the derivation of equations for lines given two points
  • Learn about setting up double integrals for non-rectangular regions
  • Explore the application of the Fundamental Theorem of Calculus in multiple dimensions
  • Practice solving double integrals with varying limits of integration
USEFUL FOR

Students and educators in calculus, particularly those focusing on multivariable calculus and double integrals, as well as anyone seeking to improve their understanding of integration over complex regions.

ineedhelpnow
Messages
649
Reaction score
0
$\int \, \int_{D}^{} \, y^3 dA$ D is the triangular region with vertices (0,1), (1,2), (4,1)

i can't get past this problem. i drew the triangle but i don't know how to find the intervals...
excuse my ugly drawing :p
View attachment 3575
 

Attachments

  • paint.png
    paint.png
    634 bytes · Views: 142
Physics news on Phys.org
ineedhelpnow said:
$\int \, \int_{D}^{} \, y^3 dA$ D is the triangular region with vertices (0,1), (1,2), (4,1)

i can't get past this problem. i drew the triangle but i don't know how to find the intervals...
excuse my ugly drawing :p
View attachment 3575

Hi! ;)

Let's start at $y=1$.
We can draw a thin horizontal rectangle there with length $4$ and height $dy$.

At $y=2$, we would have a rectangle with length $0$ and height $dy$.

Everywhere between, we have a linear transition.
That is, we have a rectangle of length $(8y-4)$ and height $dy$.

That totals to:
$$\iint_D y^3 dA = \int_1^2 y^3 \cdot (8y-4) \cdot dy$$
 
hey ils.

uuum (Blush) its a double integral though.
 
ineedhelpnow said:
hey ils.

uuum (Blush) its a double integral though.

Yep. (Nod)

So it's:
\begin{aligned}\iint_D y^3dA &= \int_1^2 \int_{\text{weird range of length $(8 - 4y)$}} y^3dx dy \\
&= \int_1^2 y^3 \left(\int_{\text{weird range of length $(8 - 4y)$}} dx\right) dy \\
&=\int_1^2 y^3 (8-4y)dy\end{aligned}
(Wasntme)
 
(Rofl) how do i find the weird range? so like $D={(x,y)|?\le x \le ?, ? \le y \le ?}$. i was looking at an example on chegg and they used the equation from side AB and BC for the interval of x. i don't remember how to get the equation of the sides of a triangle (Blush)
 
ineedhelpnow said:
(Rofl) how do i find the weird range? so like $D={(x,y)|?\le x \le ?, ? \le y \le ?}$. i was looking at an example on chegg and they used the equation from side AB and BC for the interval. i don't remember how to get the equation of the sides of a triangle (Blush)

What is the range of $x$ when $y=1$?
What if $y=2$?
And what if $y$ has some value in between those 2? (Wondering)We can also do it with the equations of AB and BC, but that is more complicated. (Doh)Anyway, for the equation of AB, we have the 2 points (0,1) and (1,2).
The equation for AB is given by:
$$y-y_A=\frac{y_B-y_A}{x_B-x_A}(x-x_A)$$
That is:
$$y-1=\frac{2-1}{1-0}(x-0) \quad\Rightarrow\quad y=x+1$$
(Wasntme)
 
thank you ils :o
yeah the reason why i asked for the equation of the line is because this lesson is about double integrals where one of the integrals is between a range of two equations and the other is between two actual numbers.
 
Another formulation would be:

$$V=\iint\limits_{R}y^3\,dA=\int_1^2 y^3\int_{y-1}^{7-3y}\,dx\,dy=\int_1^2 y^3(8-4y)\,dy$$

Just as suggested above. :D
 
i found BC and i got $x=3y-5$.
so $ \int_{y-1}^{3y-5} \ $?
 
  • #10
ineedhelpnow said:
i found BC and i got $x=3y-5$.
so $ \int_{y-1}^{3y-5} \ $?

That doesn't look right. (Worried)
How did you find it? (Wondering)
 
  • #11
i have no idea. i did it again. its x=7-3y
 

Similar threads

MHB Evaluate the surface integral $\iint\limits_{\sum}f\cdot d\sigma$
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad How do a bunch of integrals make an n-simplex or an n-cube?
  • · Replies 2 ·
Replies
2
Views
1K
MHB How do I set up double integrals for different orders of integration?
  • · Replies 4 ·
Replies
4
Views
2K
MHB The Origin of the \hat x Term in Evaluating Double Integrals over Triangles
  • · Replies 3 ·
Replies
3
Views
2K
MHB How to evaluate a double integral over a bounded region?
  • · Replies 5 ·
Replies
5
Views
2K
Graduate [Double integral] Area of a triangle
  • · Replies 1 ·
Replies
1
Views
2K
MHB How Do You Set Up Double Integrals Over a Semicircular Region?
  • · Replies 10 ·
Replies
10
Views
3K
Graduate Summing over continuum and uncountable numerocities
  • · Replies 1 ·
Replies
1
Views
3K
MHB How do you evaluate the spherical coordinate integral at 244.15.7.24?
  • · Replies 14 ·
Replies
14
Views
3K
MHB How Do You Set Up Double Integrals for Different Orders of Integration?
  • · Replies 5 ·
Replies
5
Views
2K