SUMMARY
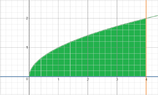
This discussion focuses on setting up double integrals for the function \( \frac{y}{1 + x^2} \) over a specified region \( R \), bounded by \( y = 0 \), \( y = \sqrt{x} \), and \( x = 4 \). Two orders of integration are established: first using vertical strips, resulting in the integral \( I = \int_0^4 \frac{1}{x^2+1} \int_0^{\sqrt{x}} y \, dy \, dx \), and second using horizontal strips, yielding \( I = \int_0^2 y \int_{y^2}^4 \frac{1}{x^2+1} \, dx \, dy \). Both setups lead to the same evaluation result of \( \frac{1}{4} \ln(17) \), confirming the consistency of the integration process.
PREREQUISITES
- Understanding of double integrals and their applications
- Familiarity with the concepts of integration order
- Knowledge of the functions \( y = \sqrt{x} \) and \( y = 0 \)
- Basic skills in evaluating integrals involving \( \frac{1}{x^2+1} \)
NEXT STEPS
- Study the properties of double integrals in different coordinate systems
- Learn about changing the order of integration in double integrals
- Explore the evaluation of integrals involving trigonometric functions, specifically \( \arctan \)
- Practice setting up double integrals for various bounded regions
USEFUL FOR
Students and professionals in mathematics, particularly those focusing on calculus, integration techniques, and anyone seeking to deepen their understanding of double integrals and their applications in different contexts.