How Do You Solve a Truss Equilibrium Problem with Incorrect Force Calculations?

[JasonR2]

Question:

Three forces of magnitude 45 kN, 24 kN and 12 kN are applied to the truss connection as shown. Knowing that the connection is in equilibrium, determine the magnitude of the forces C and T.

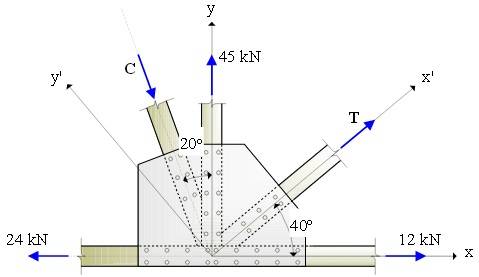
Equations:

Fx = 0
Fy = 0

My attempt:

Fx=0:

-24kN + Tcos40 + Csin20 = 0

Fy = 0:

45kN + Tsin40 - Ccos20 = 0

By substitution:

Divide first equation by sin20:

2.24T + C = 70.17 kN ---> C = 70.17kN - 2.24T (Plug that C into equation 2.)

Tsin40 - (70.17kN - 2.24T)(cos20) = -45kN

2.75T = 20.94

T = 7.62kN (Plug that back into equation 1 to find C)

C = 53.10 kN

However the answer is supposed to be C = 44.89kN and T = 4.35kN

What am I doing wrong?

 

[robphy]

How do you get your Fx equation?

 

[Shane Gribben]

For a start sign convention:
∧ +ve & >+ve

∑_v=0

-24 + CCos70 = TCos40 +12​

∑_h=0

-CSin70 = TSin40 +45

from here you should be able to get answer​

 

[greentlc]

I think you missed the 12 kN in your Fx equation. I didn't go through the math though.