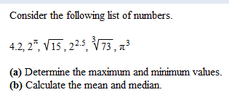SUMMARY
The discussion focuses on solving mathematical expressions where the exponent is π and involves cube roots. The identity used is \( a^{b} = e^{b \ln a} \), which allows for the transformation of expressions into a form suitable for calculation. Specific examples provided include \( e^{\ln 4.2} \), \( e^{\pi \ln 2} \), and \( e^{\frac{1}{3} \ln 73} \). The consensus is that while some cube roots can be calculated directly, most require the use of a calculator for accurate results.
PREREQUISITES
- Understanding of exponential functions and logarithms
- Familiarity with the natural exponential function \( e \)
- Basic knowledge of cube roots and their properties
- Proficiency in using scientific calculators for complex calculations
NEXT STEPS
- Study the properties of logarithms and their applications in solving exponents
- Learn how to use scientific calculators for evaluating expressions with π
- Explore advanced topics in calculus related to exponential growth and decay
- Investigate numerical methods for approximating cube roots
USEFUL FOR
Students, educators, and anyone interested in advanced mathematics, particularly in solving complex exponential equations involving π and cube roots.