Impulse
- 19
- 0
Homework Statement
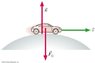
The problem motivating this post is: "An out-of-gas car is rolling over the top of a hill at speed v. At this instant,
a. n > FG
b. n < FG
c. n = FG
d. We can't tell about n without knowing v." (Associated figure attached.)
Homework Equations
[/B]
Newton's second law
The Attempt at a Solution
What I'd like to understand is in what framework to think about the normal force.
I currently understand the normal force to be equal and opposite to the perpendicular force exerted by an object on the surface with which it is in contact. I still believe this to be correct.
I'm wrestling with how to solve for the normal force. Originally, I assumed it was always equal and opposite to the perpendicular component of the force of gravity, such as is the case in a standard incline plane problem. To solve for the normal force, I would first solve for the perpendicular component of the force of gravity, then flip the sign. However, the motivating problem I posted above, as well as examining a car doing a vertical loop-the-loop and driving around a curve on a banked track, has shown that this framework for solving for the normal force can be faulty.
It now appears that, to solve for the normal force acting on an object, I should first determine the resulting motion of the object known to be true in a given scenario and then set the normal force equal to whatever force is required to make that motion result. So, in the motivating problem above, because I know the car will roll down the other side of the hill, the downward force of gravity must exceed the upward normal force, and the answer must be "b".
Is this line of thinking how you understand to solve for the normal force?
The paradigm of "first determine how you know the system to act, then set a force equal to whatever is required to make the system act in that way" feels foreign to me. I'm used to "first solve for all the forces, then determine how the system will act as a result of those forces."