Hi ehild! :)
ehild said:
It would be interesting to solve the problem directly, by integration.
ehild
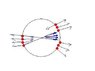
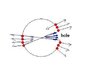
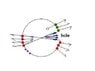
Please look at the attachment, I think of solving the problem by considering small rings on the surface of sphere.
Let the radius of sphere be R, then the radius of ring is ##R\sin\alpha##. The distance of hole from the centre of this ring is ##R(1-\cos\alpha)##. The charge contained on this ring is ##dq=\sigma dA=\sigma 2\pi R^2\sin\alpha \,\, d\alpha## where ##\sigma## is the surface charge density of sphere.
Calculating ##\sigma##:
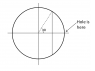
Assume that the hole subtends an angle of ##2\theta## (negligibly small) at the centre of sphere. Then the area of remaining sphere is ##4\pi R^2-2\pi R^2(1-\cos\theta)=\pi R^2(4-\theta^2)##. Hence,
$$\sigma=\frac{Q}{\pi R^2(4-\theta^2)}$$
Lets find the electric field at the hole. I use the result of electric field on the axis of ring at a distance z from the centre. The result is
$$E=\frac{kqz}{(z^2+r^2)^{3/2}}$$
In the case of selected ring, ##z=R(1-\cos\alpha)## and ##r=R\sin\alpha##. Substituting and simplifying:
$$dE=\frac{k\sigma \pi}{\sqrt{2}}\frac{\sin\alpha}{\sqrt{1-\cos\alpha}}d\alpha$$
Integrating the above with limits for ##\alpha## from ##\theta## to ##\pi##, we get:
$$E=2k\sigma \pi(1-\sin(\theta/2))=\frac{2kQ}{R^2}\frac{1-\sin(\theta/2)}{4-\theta^2}$$
I evaluated the series expansion at ##\theta=0## using wolfram alpha.
http://www.wolframalpha.com/input/?i=series+expansion+(1-sin(x/2))/(4-x^2)+at+x=0
Neglecting the terms containing ##\theta##, we are simply left with ##1/4## i.e
$$E=\frac{2kQ}{R^2}\frac{1}{4}=\frac{Q}{8\pi \epsilon_{\circ} R^2}$$
Does this look good? :)
They were still red in the first picture. 
, in order to be specific .