How Does an Exploding Firework Affect Projectile Landing Distance?

[kenau_reveas]

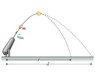
A mortar fires a shell of mass m at speed v0. The shell explodes at the top of its trajectory (shown by a star in the figure) as designed. However, rather than creating a shower of colored flares, it breaks into just two pieces, a smaller piece of mass 1/5 m and a larger piece of mass 4/5 m. Both pieces land at exactly the same time. The smaller piece lands perilously close to the mortar (at a distance of zero from the mortar). The larger piece lands a distance d from the mortar. If there had been no explosion, the shell would have landed a distance from the mortar. Assume that air resistance and the mass of the shell's explosive charge are negligible.

Find the distance d from the mortar at which the larger piece of the shell lands.

Express d in terms of .

 

[srnj222]

The center of mass of the shell will continue on the initial trajectory:

cm = ((1/5)m*0 + (4/5)m*d)m

cm = (4/5)d

d = (5/4)cm where cm is the position it owuld have landed at

 

[kenau_reveas]

it says express d in terms of r. is this d is in terms of r?

 

[srnj222]

it says express d in terms of r. is this d is in terms of r?

if r is the position it would have landed at