How does BTU convert to heat in degrees in a greenhouse?

In summary, BTU (British Thermal Unit) is a measurement of heat energy that can be converted to degrees in a greenhouse by understanding the relationship between BTUs and temperature change. One BTU raises the temperature of one pound of water by one degree Fahrenheit. In a greenhouse, the effective conversion involves calculating the total BTUs required to achieve a desired temperature increase, factoring in variables such as greenhouse size, insulation, and heat loss. This conversion helps in determining the necessary heating requirements to maintain optimal conditions for plant growth.
  • #1
gary350
274
66
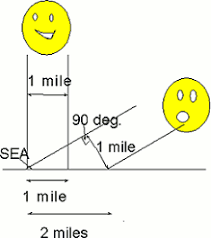
Information online claims sun is 200 btu per sq ft in winter only when sun is perpendicular to plastic or glass of a green house. When sun hits glass or plastic at an angle there are losses. The steeper the angle the more losses will be.

Is it possible to calculate how warm a green house will get in full sun at solar 12 noon.?

Our average day temperature is now about 50 degrees a temperature rise for 25 degrees will make it 75 degrees in a green house tunnel during the day only. It will still get 25 degrees after dark. Winter plants are good down to 0 to -20 degrees but nothing grows below 40 degrees.

If I can prove on paper this will work then i will build it.
100_8421.JPG
download.png
 
Last edited:
Physics news on Phys.org
  • #2
Why not build a test model with some sort of thermometer inside that can be read visually from the outside?

One thing to be aware of is snow or cloud cover may further reduce its effectiveness.

In Texas, we would cover our plants with plankets. However where the plant leaves touched the planket we would see the effects of frost.
 

FAQ: How does BTU convert to heat in degrees in a greenhouse?

What is a BTU?

A BTU, or British Thermal Unit, is a unit of measurement for heat energy. It is defined as the amount of heat required to raise the temperature of one pound of water by one degree Fahrenheit at sea level.

How does BTU relate to temperature in a greenhouse?

In a greenhouse, BTU is used to quantify the amount of heat energy needed to maintain or increase the temperature of the air and plants. The total BTU required can be calculated based on the volume of the greenhouse, the desired temperature increase, and the insulation properties of the greenhouse materials.

How do you convert BTUs to degrees Fahrenheit in a greenhouse?

To convert BTUs to degrees Fahrenheit, you need to know the specific heat capacity of air and the volume of air in the greenhouse. The formula to calculate the temperature increase is: Temperature Increase (°F) = BTU / (Volume of Air (cubic feet) × 0.018). This gives you the increase in temperature based on the amount of heat energy supplied.

What factors affect the conversion of BTUs to heat in a greenhouse?

Several factors affect the conversion of BTUs to heat in a greenhouse, including the greenhouse's size, the insulation quality, the outside temperature, humidity levels, and the heat retention characteristics of the materials used. These factors determine how efficiently the BTUs are converted into heat energy that raises the temperature inside the greenhouse.

How can I calculate the BTU requirements for my greenhouse?

To calculate the BTU requirements for your greenhouse, you can use the formula: BTU = Volume of Greenhouse (cubic feet) × Temperature Difference (°F) × Insulation Factor. The insulation factor accounts for heat loss through the greenhouse materials. This calculation will help you determine how much heating capacity you need to maintain your desired temperature.

Similar threads

A Average temperature in a greenhouse
Replies
2
Views
1K
How does the loss of sea ice affect Earth's temperature?
2
Replies
42
Views
5K
Calculating BTU for Heating a Garage from 40 to 60°F in 4 Hours
2
Replies
41
Views
4K
Is greenhouse interior much cooler if reflective inside?
Replies
1
Views
1K
Thermodynamics: Calculating Outside Temperature of a Greenhouse with Heat Loss
Replies
1
Views
1K
I Growing food in space - a 3rd concept
Replies
1
Views
1K
Can IR Heating Be Effectively Focused Over Long Distances for Snow Prevention?
Replies
18
Views
2K
Calculating Home Heat Losses for Window Replacement | 30% Tax Credit Ends Soon!
Replies
23
Views
7K
How do I compare indoor and outdoor relative humidity levels?
Replies
2
Views
2K
How do I calculate BTU? (for a water heater project)
Replies
2
Views
36K

Hot Threads

Recent Insights

Back
Top