How does combining spin result in the total spin angular momentum number?

[mk_gm1]

I was wondering if someone could help me to understand how you combine spin to form the total spin angular momentum number, S. Here's a selection from my notes:

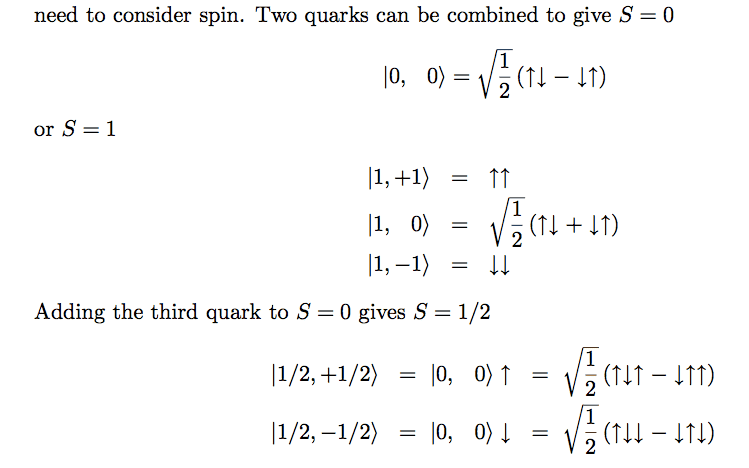
Now as I understand it, S = (s_1 + s_2), (s_1 + s_2 - 1), ... |s_1 - s_2|. However, I don't really see how that leads to the conclusion that the singlet state above has S=0 and the triplet state has S=3.

And even if I can find a way to rationalise it for the 2 quark case, I don't have a clue what's going on when you add the third quark to S=0. I mean, I get that the spin of a quark is 1/2 so adding it to S=0 gives you S=3/2, but I don't see how S=1/2 corresponds to the states:

\frac{1}{\sqrt{2}} \left(\uparrow \downarrow \uparrow - \downarrow \uparrow \uparrow \right) and \frac{1}{\sqrt{2}} \left(\uparrow \downarrow \downarrow - \downarrow \uparrow \downarrow \right)

Could someone kindly explain this to me?

 

[kanato]

Recall that S^2 and S_z commute, and these sorts of states are eigenstates of those operators.

Define the total spin operator S = S_1 + S_2. Then you want to calculate the value of S^2:
S^2 = S_1^2 + S_2^2 + 2 S_1 \cdot S_2

Then compute the action of S^2 in each state, recalling for an eigenstate that
S^2 |Sm\rangle = s(s+1) |Sm\rangle

Don't forget the identity
S_1 \cdot S_2 = S_1^z S_2^z + \frac12(S_1^+ S_2^- + S_1^- S_2^+)

You should be able to compute the eigenvalue S for each state and get the result you've posted.

 

[mk_gm1]

Thank you for your reply. I'm afraid I'm having some problems with the maths. Let's take the triplet ^^.

Define the spin state, \chi = \uparrow_1 \uparrow_2.

S^2 \chi = S_1^2 \chi + S_2^2 \chi + 2 S_1 \cdot S_2 \chi

S_1^2 \chi = S_2^2 \chi = \frac{3}{4} \hbar^2 \chi

S_{1z} S_{2z} \chi = \frac{1}{2} \cdot \frac{1}{2} \hbar^2 \chi

S^\pm = \hbar \sqrt{s(s+1)-m(m \pm 1)} = \hbar \sqrt{\frac{3}{4} - \frac{1}{4} \mp m}

because we're dealing with spin half particles that have values of m = \pm \frac{1}{2} . Hence,

S^2 \chi = \frac{3}{2} \hbar^2 \chi + \frac{1}{2} \hbar^2 \chi + \hbar^2 \left(\frac{3}{4} - \frac{3}{4} \right)\left(\frac{3}{4}\right) \chi + \hbar^2 \left(\frac{3}{4} \right)\left(\frac{3}{4}- \frac{3}{4} \right) \chi

Therefore

S^2 \left(\uparrow_1 \uparrow_2 \right) = 2 \hbar^2 \chi.

Edit: Realised my mistake. Woops.

 

[diggy]

My recollection was that singlet state is a 1/2 one way and the other 1/2 the opposite way (essentially a spin 0 particle). Total z component of the spin, m, can then only be 0.

The triplet state is 1/2 plus 1/2, for a total spin is 1 and its m can be -1, 0, 1. A particle with spin=1 (by itself) also uses the triple (m=-1,0,1) form. The key note here is that S=1 not 3, the triplet refers to the number of possible z configurations.

A particle with net spin 1/2, such as a quark or proton (where the spin goes 1/2 for first quark (doublet state), to 0 for first + second quark (either singlet or triplet as described above), and finally 1/2 (doublet) again for all quarks), only has 2 allowed m states, +1/2 and -1/2. If the 3 quarks of the proton all line up its a called a delta. The delta's total S is 3/2, so it can have 4 m states, +3/2,+1/2, -1/2, -3/2.

Its a lot easier if you think of it in pictures, then do the math.

 

[mk_gm1]

My recollection was that singlet state is a 1/2 one way and the other 1/2 the opposite way (essentially a spin 0 particle). Total z component of the spin, m, can then only be 0.

The triplet state is 1/2 plus 1/2, for a total spin is 1 and its m can be -1, 0, 1. A particle with spin=1 (by itself) also uses the triple (m=-1,0,1) form. The key note here is that S=1 not 3, the triplet refers to the number of possible z configurations.

A particle with net spin 1/2, such as a quark or proton (where the spin goes 1/2 for first quark (doublet state), to 0 for first + second quark (either singlet or triplet as described above), and finally 1/2 (doublet) again for all quarks), only has 2 allowed m states, +1/2 and -1/2. If the 3 quarks of the proton all line up its a called a delta. The delta's total S is 3/2, so it can have 4 m states, +3/2,+1/2, -1/2, -3/2.

Its a lot easier if you think of it in pictures, then do the math.

Thanks for the reply. I realized I made a really stupid mistake in my maths which I fixed and then it all came out.

With regards to picturing it, I can see why that's useful for a singlet/triplet state when you're dealing with 2 particles. But I don't think I could intuitively look at a state udu - duu and say immediately that it corresponds to S, M_s of +1/2, +1/2.

Out of interest, how do you extend the following identity to N particles?

S_1 \cdot S_2 = S_1^z S_2^z + \frac12(S_1^+ S_2^- + S_1^- S_2^+)

 

[diggy]

Its easier to think of visually because these are all vectors, and what you want at the end is just the sum of the vectors (in whatever orientation they line up in).

d= -u , so u+d=0 (that's all in made up vector notation)

its just like saying I walk across the room and back. Then when you add the third particle, its the whole vector (in the case of protons and neutrons).

For the case of N, s=1/2, l=0 objects, I believe the solution is basically derived the same as the N=2 case

(S₁+ S₂+ S₃ +...)² = S₁² + S₂² + S₃² + 2*S₁\dotS₂ + ...

In the udu case one S1 and S2 cancel, leaving just S3, a spin 1/2 object, that can have m=+1/2 or m=-1/2

Check out any modern textbooks laying around (or nuclear), they will have the pictures that make it clearer than I can type. But basically the only quantum stipulation is the size of the vectors and the quantization in z (or whatever you eigenvalue you are using). After that its just regular vector addition. Same when you do J=L+S.