How does L from LU give us column space?

[LongApple]

I see that the pivots in columns 1 and 2 help us decide which columns to take. But why does the L matrix of this B = LU let just to read off the column space?

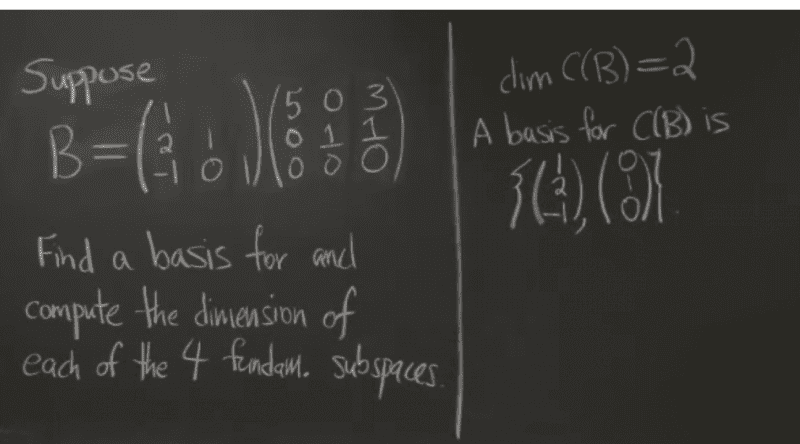
2:18

 

[jbunniii]

The column space of $B$ is the set of all $Bx$, where each $x$ is a $3 \times 1$ vector whose elements are the coefficients of a particular linear combination of the columns of $B$.

If $B = LU$, then $Bx = LUx = L(Ux) = Ly$, so any linear combination of the columns of $B$ is also a linear combination of the columns of $L$. This means that $C(B)$ (the column space of $B$) is a subspace of $C(L)$ (the column space of $L$).

In this case, $C(B)$ is a proper subspace of $C(L)$, which we can see by arguing as follows. By inspection, the columns of $L$ are linearly independent, so $L$ is invertible. This means that the null space of $B$ is the same as the null space of $U$, because invertibility of $L$ implies that $LUx = 0$ if and only if $Ux = 0$. Since $U$ has two linearly independent columns, $U$ has rank 2, so the dimension of $N(U) = N(B)$ is 1. Therefore $C(B)$ has dimension 2, whereas $C(L)$ has dimension 3.

Moreover, by examining $U$ we can see that $C(U)$ consists exactly of vectors of the form $(a,b,0)^T$, since the third row of $U$ is zero. This means that only the first two columns of $L$, namely $(1,2,-1)^T$ and $(0,1,0)^T$ contribute to the column space of $B$. Since these two columns are linearly independent and $C(B)$ has dimension 2, they form a basis for $C(B)$.