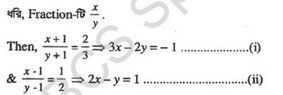SUMMARY
The discussion centers on solving a system of equations derived from modifying the numerator and denominator of a fraction. The equations presented are 3x - 2y = -1 and 2x - y = 1, which arise from the conditions that adding 1 to both the numerator and denominator results in 2/3, and subtracting 1 results in 1/2. The solution involves substituting y from the second equation into the first to isolate x, ultimately leading to the values of x and y that satisfy both equations.
PREREQUISITES
- Understanding of algebraic equations and systems of equations
- Familiarity with fraction manipulation and properties
- Knowledge of substitution methods in solving equations
- Basic skills in arithmetic operations involving fractions
NEXT STEPS
- Study methods for solving systems of linear equations, particularly substitution and elimination
- Explore the properties of fractions and how modifications affect their values
- Learn about graphical representations of linear equations and their intersections
- Practice solving word problems that involve fractions and algebraic equations
USEFUL FOR
Students, educators, and anyone looking to enhance their understanding of algebra, particularly in solving equations involving fractions and systems of equations.