How Does Rotating Polarization Work in Optics Experiments?

[ynyin]

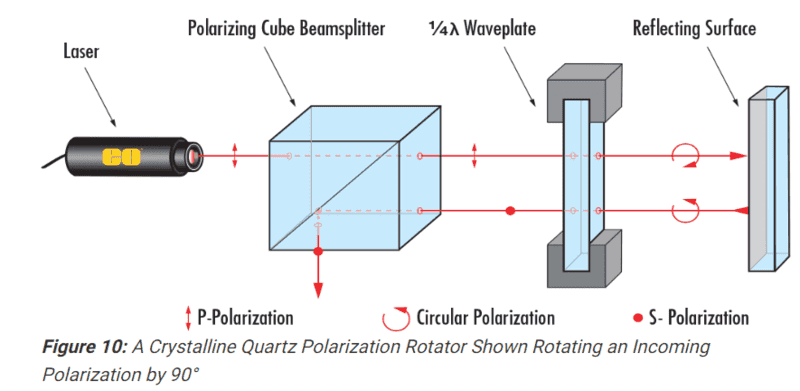
In optics experiments, I often see the following optics configuration to rotate the polarization of an incident linearly-polarized laser beam. The final reflected beam has its polarization rotated by 90 degrees. My question is:
1) Between the quarter plate and the mirror( reflecting surface), the following figure indicates the handness of the circular polarization does not change when it is reflected back. But from what I learned, the polarization should change its handness while being reflected by a mirror. (see, e.g. this question: https://physics.stackexchange.com/q...se-polarization-of-circularly-polarised-light)

2) If the circular polarization changes its handness, then after the quaterplate it should become the same linear polarization as the incident laser beam, meaning that it should pass through the PBS again and not be refleted away.

Where could I be wrong in understanding its principle? Thanks!

 

[vanhees71]

I'd need a bit more context to understand the depicted optical setup. Where is the picture from?

 

[ynyin]

I'd need a bit more context to understand the depicted optical setup. Where is the picture from?

Thanks for the reply. There are quite some occasions where this optics configuration is used, see, for example:
1) The picture is from Figure 14 in this link:
https://www.edmundoptics.com/knowledge-center/application-notes/optics/understanding-waveplates/

2) http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/cdopt.html#c3

3) http://www.jg-intl.com/cp/html/?85.html

 

[vanhees71]

Through 2) it became clear what the picture in 1) means: You have an incoming unpolarized beam hitting a polarizing beam splitter (PBS) and use one of the beams, which now is linearly polarized. This linearly polarized light goes through a quarter-wave plate (QWP) making it circular polarized. Depending on the polarization of the used linearly polarized beam (H or V) the outgoing beam is L or R circular polarized after the QWP. The now circular polarized beam is reflected. Circular polarization means the light is in a helicity eigenstate, and a reflection flips helicity. The reason is that helicity is a pseudoscalar: Helicity is $\vec{k} \cdot \vec{J}/|\vec{k}|$, where $\vec{k}$ is the wave vector and $\vec{J}$ the angular momentum of the electromagnetic wave. Under a reflection $\vec{k}$ flips sign (polar vector), while $\vec{J}$# doesn't (axial vector). Thus if you have a L (R) circular polarized incoming beam the relected one is R (L) polarized. Now this goes again through the QWP making it linearly polarized in the perpendicular direction than that of the before incoming beam. At the PBS it still stays in this same perpendicular direction, i.e., the entire apparatus rotates the polarization by an angle of $\pi/2$.

 

[ynyin]

Through 2) it became clear what the picture in 1) means: You have an incoming unpolarized beam hitting a polarizing beam splitter (PBS) and use one of the beams, which now is linearly polarized. This linearly polarized light goes through a quarter-wave plate (QWP) making it circular polarized. Depending on the polarization of the used linearly polarized beam (H or V) the outgoing beam is L or R circular polarized after the QWP. The now circular polarized beam is reflected. Circular polarization means the light is in a helicity eigenstate, and a reflection flips helicity. The reason is that helicity is a pseudoscalar: Helicity is $\vec{k} \cdot \vec{J}/|\vec{k}|$, where $\vec{k}$ is the wave vector and $\vec{J}$ the angular momentum of the electromagnetic wave. Under a reflection $\vec{k}$ flips sign (polar vector), while $\vec{J}$# doesn't (axial vector). Thus if you have a L (R) circular polarized incoming beam the relected one is R (L) polarized. Now this goes again through the QWP making it linearly polarized in the perpendicular direction than that of the before incoming beam. At the PBS it still stays in this same perpendicular direction, i.e., the entire apparatus rotates the polarization by an angle of $\pi/2$.

Thanks for the explanation! The flipping of the handness of the circular polarization (from L to R or R to L) is something I have thought about, and that is why I think the figure shows the circular polarization wrongly. The question now is why after QWP the linear polarization is perpendicular to that of the incoming beam. Fortunately, I got the answer from StackExchange, the key point is that the reflected beam sees the fast axis of the QWP at an angle rotated by 90 degrees w.r.t what it sees when it is incoming. Hope that also clarifies something for you.

 

[vanhees71]

Sure, we seem to agree.