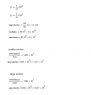How Does Shaft Diameter Affect Power Transmission and Torque?

[MMCS]

A shaft runs at 300 rev/min and transmits power from a pulley A at one end to two
pulleys, B and C, which each drive a machine in a workshop. The distance between
pulleys A and B is 3 m and that between B and C is 2.4 m (i.e. the total length of the
shaft is 5.4 m). The shaft has a diameter of 50 mm between A and B and a diameter
of 40 mm between B and C. If the maximum permissible shear stress in the shaft is 80
MPa, calculate the maximum power which may be supplied from each of the pulleys B
an C, assuming that both machines would be in operation at the same time. Also
calculate the total angle of twist of one en
d of the shaft relative to the other when
running on full load. G = 80 (GPa)

Answers:
(30.2 kW; 31.4 kW; 13.7°)


Attached is my working, i can arrive at the answer of 31.4KW for the pulley at C at the smaller diameter step, however when i try the same calculate with the second moment of area (J) for the larger diameter i get an answer in excess of 60000KW. How would i calculate the torque for the larger diameter section?

as you can see from my working I've used the standard formula rearranged for torque, then used the standard power equation.

Thanks

 

[CWatters]

Here is a diagram of the set up..

Relevant Equations:
Power = T * ω .....(1)
where
T = Torque in Nm
ω = Angular velocity in Rads/S

The Polar Second Moment of Area (J) for a solid round shaft is
J = πd⁴/32......(2)
where d is the diameter in meters.

Max Stress τ_max = Td/2J....(3)

Substitute (2) into (3) and rearrange to give an equation for the Max Torque in terms of the Max Stress..

T = (τ_max * π * d³)/16...(4)

Shaft from B to C

Now we can calculate the max torque and power allowed in the section of shaft from B to C...

Using (4) and...

τ_max = 80 * 10⁶Pa
d = 0.04m

T = (80*10⁶ * π *0.04³)/16
= 1005Nm

Then using (1) we can calculate the max power

Power_C = 1005 * 300 * 2π/60
= 31.6kW
This is slightly higher than the book answer of 31.4kW. Looks like they rounded the Torque down to 1000Nm.

Shaft from A to B

Now we can calculate the max torque in the section of shaft from A to B and the power available at B...

Using (4) and...

τ_max = 80 * 10⁶Pa
d = 0.05m

T = (80*10⁶ * π *0.05³)/16
= 1963Nm

However this time to calculate the power available at B we must subtract the torque required at C ..

T = 1963 - 1005 = 958NM

Then using (1) we can calculate the max power that can be delivered to machine B..

Power_B = 958 * 300 * 2π/60
= 30.1kW
This is fractionally lower than the book answer of 30.2kW. I haven't tried to account for the difference.

 

[CWatters]

Angle of Twist

Relevant Equations

The angle of twist in each section is given by
θ = TL/GJ......(5)

where
T = Torque
L = Length
J = Polar Second Moment of Area of that section

From my post above..
J = πd⁴/32......(2)

Substituting for J in (5)...

θ = 32TL/Gπd⁴

For the section AB

T = 1963Nm
L = 3m
d = 0.05m
G = 80 * 10⁹Pa

so

θ_AB = (32 * 1963 * 3) / (80 * 10⁹ π * 0.05⁴)

= 0.12 Rads
= 6.8 degrees

For the section BC

T = 1000Nm
L = 2.4m
d = 0.04m
G = 80 * 10⁹Pa

so

θ_AB = (32 * 1000 * 2.4) / (80 * 10⁹ π * 0.04⁴)

= 76800 / 643398
= 0.12 rADS
= 6.8 degrees same as section AB

Total Twist = 6.8 + 6.8 = 13.6 degrees