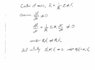How Does the Center of Mass Move in a Block and Wedge System?

[blackwing1]

Homework Statement

A large wedge rests on a horizontal frictionless surface. A block starts from rest and slides down the inclined surface of the wedge, which is rough. During the motion of the block, the center of mass of the block and wedge.

a. does not move.
b. moves horizontally with constant speed.
c. moves horizontally with increasing speed
d. moves vertically with increasing speed
e. moves both horizontally and vertically

The correct answer was d.

Homework Equations

None given.

The Attempt at a Solution

I reasoned that since the block would begin to slide down the inclined plane, the center of mass of the entire system would shift in relation to the position of the block. Therefore, the center of mass should move both horizontally and vertically.

 

[Spinnor]

Does the following make any sense?

 

[Spinnor]

Does the following make any sense?

I'm missing some minus signs. m1v1 not equal m2v2 should read m1v1 not equal -m2v2 and m1v1 = m2v2 should read m1v1 = -m2v2

 

[blackwing1]

Thanks for helping :D
However, I still don't get it. What exactly is M_1, M_2 and V_1 and V_2 in this case, and how do the initial equations arrive at the conclusion through the arrows? Could you please elaborate? I kind of see how the math works, but I don't know how it arrives at the conclusions. Also, would you happen to know of another way to solve this problem? The test that I'm taking this from was supposed to be non-calculus based, so would you happen to know an algebraic way to solve it too?

Once again, thanks.

 

[ehild]

To answer the problem, you need to know how the CM is defined, and how the acceleration of the CM is related to the forces acting on the system.

ehild