Acceleration of a block on a moving wedge

[fontseeker]

Homework Statement

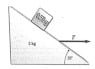
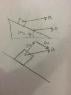
A block of mass 0.5Kg rests on the inclined surface of a wedge of mass 2kg. The wedge is acted on by a horizontal force that slides on a frictionless surface. If the coefficient of static friction between the wedge and the block is 0.8 and the angle is 35 degrees, find the maximum and minimum values of F for which the block does not slip.

Homework Equations

F = ma

The Attempt at a Solution

I don't fully understand how to apply the acceleration of the wedge to the block. I know both objects are traveling with the same acceleration, but then wouldn't that mean that the block is moving with an acceleration down the ramp?

 

[scottdave]

The way you have drawn your sketch implies that a_y lifting off from the wedge and a_x accelerating down the wedge is not what is happening. In fact, there is no acceleration between the block and wedge.
Try starting to look at the block and the wedge when there is no force pulling the wedge. Think about the following:

• What forces are acting on the block?
• What is the amount of frictional force necessary to keep it in place?
• How much additional Normal force is required to get the necessary frictional force.
• When the external force is applied, how does that transfer to additional forces applied to the block?

 

[rude man]

Sum forces up and down the ramp and set =ma where m = mass and a = accel. of block. Do this twice, considering the friction force could act as to push the block either up or down the ramp

Hint: F could be negative!
.

 

[fontseeker]

Sum forces up and down the ramp and set =ma where m = mass and a = accel. of block. Do this twice, considering the friction force could act as to push the block either up or down the ramp

Hint: F could be negative!
.

I've done the summation of forces uses the incline as my x-axis for both friction going up and down. However, how would I incorporate the acceleration of the wedge?

 

[rude man]

I've done the summation of forces uses the incline as my x-axis for both friction going up and down. However, how would I incorporate the acceleration of the wedge?

Remeber ΣF = ma? What's a along the incline & how does it relate to F?

 

[fontseeker]

Remeber ΣF = ma? What's a along the incline & how does it relate to F?

Wouldn't a along the incline have to be 0 in order for the block not to slide?

 

[rude man]

Wouldn't a along the incline have to be 0 in order for the block not to slide?

I'm changing my answer somewhat.

Yes, with respect to the incline there is zero acceleration - zero motion in fact. But the equation ΣF = ma applies in an inertial, not accelerating, coordinate system. In an inertial refrence system the block and wedge are both accelerating = a. But you can sum forces in the direction of the incline and let those sum to m times acceleration of the block in the direction of the incline but realize that acceleration along the direction of the incline is not the same as acceleration along the directon of a.

(In fact you can think of F as being replaced by another force F' = -ma, then the block experiences zero net acceleration so now ΣF' = 0, F' = F - ma. This is known as d'Alembert's principle which you may run into in a later dynamics course.)

A similar scenario is say you're in an elevator & the cables broke & you're dropping with acceleration -g. If you were to try to drop an item from your hand the item would have no motion with respect to you but of course you & the item are both accelerating at -g in inertial space. Same with the block and the wedge.