How Does the Infinite Potential Well Illustrate the Uncertainty Principle?

[omri3012]

infinite potential well and the uncertainty principle

the solution for Schroedinger equation in infinite potential well satisfy the following

energy levels:

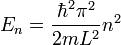
where l is the width of the well.

E can't be zero since then \psi=0 so there isn't any particle in the well . i read in

a book that "there is a tight connection between this fact (E\neq0) and the

uncertainty principle", what exactly is the connection?

 

[neworder1]

I don't know what the author meant, but my guess would be:
- since the well has finite width, the uncertainty in position is always finite, i.e. \Delta X < \infty
- now, if you take time-independent Schroedinger equation H\Psi=E\Psi \Leftrightarrow \frac{\partial^2 \Psi}{\partial x^2}=\frac{-2mE}{\hbar^2}\Psi and put this into momentum uncertainty: \langle P^2 \rangle - \langle P \rangle^2 and calculate the integrals, you obtain that (\Delta P)^2 is something like \frac{-2mE}{\hbar^2}. So E=0 would violate uncertainty principle, since for E=0 \Delta P = 0, \Delta X < \infty

 

[omri3012]

Thanks for your time, i really appreciate it.

but i didn't understand two things:

1. how can you assume that H\Psi=E\Psi?

2. why does \Delta X < \infty imply for contradiction in the uncertainty principle?

 

[neworder1]

Ad. 1. When trying to determine possible energy values, we look first for a separated solution to the Schrödinger equation, i.e. solution of the form \psi (x, t) = \Psi (x) \phi (t). If the Hamiltonian H is time-independent, separation of variables proves that H\Psi = E\Psi for some constant E (look this part up in any textbook). Now we have to determine possible values of E, and the argument above show that we cannot have E=0. This is actually a bit of an overkill, since the equation \frac{\partial^2 \Psi}{\partial x^2}=0, along with boundary conditions \Psi (0)=\Psi(L)=0, gives \Psi = 0 instantly, but I guess this is what the author had in mind.

Ad. 2. The uncertainty principle says that \Delta X \Delta P \geq \frac{\hbar}{2}. For E=0 we get \Delta P=0 as well, so the uncertainty principle could be satisfied only if \Delta X = \infty. But the well has finite width, so position uncertainty is also finite.

Obviously, this is a very roundabout way of proving that E \neq 0.

 

[omri3012]

Thanks,

now it's all clear