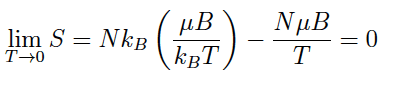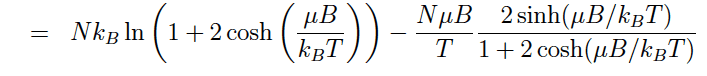Discussion Overview
The discussion revolves around the limits of the hyperbolic functions sinh and cosh as their argument approaches infinity, particularly in the context of a physical expression involving temperature and magnetic fields. Participants explore how these limits relate to logarithmic expressions and the behavior of these functions as certain parameters approach zero.
Discussion Character
- Technical explanation, Mathematical reasoning, Conceptual clarification
Main Points Raised
- One participant questions how the limit of ln(infinity) relates to the expression uB/KbT and seeks clarification on how sinh and cosh approach 1.
- Another participant asserts that both sinh(x) and cosh(x) approach e^x as x approaches infinity, suggesting that the 1 term becomes negligible compared to the cosh term.
- A participant reiterates the previous point about the limits of cosh and e^x, indicating that as x approaches infinity, both functions approach infinity, leading to the conclusion that lim(x->infinity) cosh(x) equals lim(x->infinity)e^x.
- One participant provides a mathematical expression showing that as T approaches 0, ln(1 + 2cosh(μB/kBT)) approximates to μB/kBT.
- A participant explains that in the expression for cosh(x), the e^(-x) term becomes negligible compared to the e^x term as x approaches infinity.
Areas of Agreement / Disagreement
Participants express similar views regarding the behavior of cosh and sinh as their arguments approach infinity, but the discussion remains unresolved regarding the specific limit of ln(infinity) and its relation to the other expressions mentioned.
Contextual Notes
There are unresolved assumptions regarding the definitions and limits involved in the expressions, particularly concerning the transition from logarithmic to hyperbolic functions and the implications of temperature approaching zero.