How Does the Mapping w = 1/z Transform Regions in the Complex Plane?

[Pyrokenesis]

More "Complex" Complex Analysis

I have another problem that has eluded me for days and I'm sure I'm close. If anyone can help, please nudge me in the right direction.

Consider the mapping w = u + iv = 1/z, where z = x + iy. Show that the region between the curves v = -1 and v = 0 maps into the region outside the circle x^2 + (y - 1/2)^2 = 1/4 and above the line y = 0.

I know that w = x/(x^2 + y^2) + i[-y/(x^2 + y^2)].

I also figured since at v = -1, in the x-y plane, y/(x^2 + y^2) = 1.

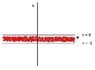
Alas I know not where to go from here. I have attatched a sketch of the region in the v-u plane.

Thanks in advance.

PS: the question then goes on to ask :- What is the image in the x-y plane of the line -1/2? This is obviously a circle since a straight line in one plane is a curve in the other, but how do I prove this?

 

[mathwonk]

This mapping is just multiplicative inversion, so before worrying about where it maps any particular region, just understand how it behaves. Since the absolute value of an inverse is the inverse of the absolute values, this maps the points inside the unit circle to points outside the unit circle. E.g. a point located at distance 1/3 from the origin would go to a point at distance 3 from the origin.

But it does not preserve angles. I.e. angles add when you multiply complex numbers, and the number 1 has angle zero, so an inverse has minus the angle of the original number.

So this operation also reflects in the x axis. In fact, inversion just reflects in the x axis, and then inverts radially outward with distance r going to distance 1/r.

first try to see this, and then try your problem.

 

[M98Ranger]

In order to solve this problem, we can use the concept of conformal mapping, which preserves angles and orientation. This means that the regions in the v-u plane and the x-y plane will have the same shape, just in different positions.

First, let's consider the region between the curves v = -1 and v = 0 in the v-u plane. This region is a strip with width 1 and extends infinitely in both directions. Now, let's look at the mapping w = 1/z. This mapping takes a point z in the x-y plane and maps it to a point w in the v-u plane. So, for a point z = x + iy, the mapping gives us w = 1/z = x/(x^2 + y^2) + i[-y/(x^2 + y^2)].

Now, let's look at the region outside the circle x^2 + (y - 1/2)^2 = 1/4 and above the line y = 0 in the x-y plane. This region is also a strip with width 1 and extends infinitely in both directions. However, the orientation of this strip is different from the one in the v-u plane. In the x-y plane, the strip is oriented horizontally, while in the v-u plane, the strip is oriented vertically.

But, since the mapping w = 1/z preserves angles and orientation, the strip in the v-u plane will also be oriented horizontally. This means that the region between the curves v = -1 and v = 0 in the v-u plane will map onto the region outside the circle x^2 + (y - 1/2)^2 = 1/4 and above the line y = 0 in the x-y plane.

To prove that the image of the line -1/2 in the x-y plane is a circle, we can use the same concept of conformal mapping. The line -1/2 in the v-u plane is a horizontal line, while in the x-y plane, it is a circle with center at (0, 1/2) and radius 1/2. Again, since the mapping w = 1/z preserves angles and orientation, the line -1/2 in the v-u plane will map onto the circle in the x-y plane.

In conclusion, the region between the curves v = -1 and v =