Janusz Bednarski
- 5
- 0
- Homework Statement
- How can one use a quantum well to change the colour of emitted light from an LED without changing the semiconductor material?
- Relevant Equations
- -
Hi!
This question is translated so that's why it might sound a bit weird. I know that the answer should mention the band diagram of the LED, and I think that the answer is to introduce an electrical contact connected to a voltage source. Then when you increase the voltage, it should attract the electrons from the quantum well, and repel the holes from the other well, thus increasing the band gap and increasing the emitted light's energy (different colour). And vice versa for a negative voltage.
Am I correct?
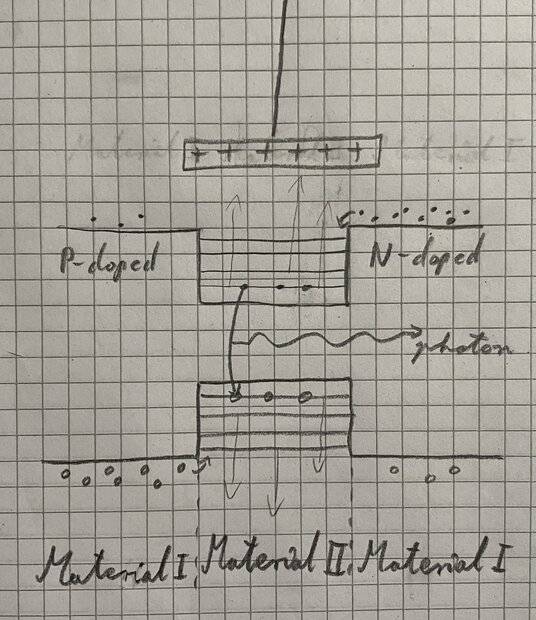
This question is translated so that's why it might sound a bit weird. I know that the answer should mention the band diagram of the LED, and I think that the answer is to introduce an electrical contact connected to a voltage source. Then when you increase the voltage, it should attract the electrons from the quantum well, and repel the holes from the other well, thus increasing the band gap and increasing the emitted light's energy (different colour). And vice versa for a negative voltage.
Am I correct?