- #1
Curiose
- 18
- 2
[Mentors' note: one short paragraph of speculation in violation of the Physics Forums rules has been removed from this post]
Follow the link below to play with my experimental sandbox. The rest of this post includes some instructions for use and then observations and a little bit of theory.
WaveGrid Demo - play with the simulator here, but read at least enough of what's below to understand it ;)
I took an open source art project written by someone else and turned it into a simulator of a 4D dynamical system, which you can "paint" on. Original code can be found on rectangleworld here
The part I liked about the original project is that the guy represented a 3D boids simulation using the actual "local neighborhood" as a continuous 2D grid through which the cells are arranged visually like cellular automata. One emergent feature I saw in rendering boids like this was that you could actually observe a wave-like behavior in the 2D grid, since the 3D location was represented as an (R,G,B) color. So it's structure is (X,Y,Z) = (GridX, GridY, (R, G, B))
Most people when trying to visualize the boids algorithm use just the plain x,y,z coordinates... and in order to make the algorithm more "true-to-form", they attempt to use a partitioning algorithm (like kdTree) in order to find a local neighborhood on each frame. The default alternative was to generate a pre-calculated local neighborhood as was the case with the original manifestation of the algorithm. So the author simply took this apparent error and turned it into an advantage.
In the Algorithm, each individual boid is linked to it's 8 surrounding neighbors upon initialization forming a lattice by which they share their location point in each dimension as well as their n-dimensional velocity vector. Technically each boid on each frame "observes" it's neighbors and uses that observational data to recalculate it's own velocity vector, which is in turn, observed by each of it's neighbors (a . The great part about the Grid (or the observational matrix) is that through the grid you can see how the different colors interact with each other. Using this method, higher than 3 dimensions can be represented visually through a 2D grid. The other advantage is that technically two boids can occupy the same exact point in 3D space without reacting to each other, which when extrapolated to the 2D view, means that two cells can be the same exact color, which, when using partitioning, is not possible.Usage
The grid starts out with all boids being "Grey" with 0 ease {r: 127, g: 127, b: 127, e: 0}. The 4D velocity vector of each boid is set to 0.
Along the bottom of the view, you have colors, as well as a global ease setting and a couple of other options. The colors are set up in a way that black,white is one group, then the elemental colors R, G, and B. After that are the mixed colors like cyan, magenta and yellow. These colors are secondary colors to the R,G,B space because they include a mix of maximum intensity of two colors and 0 intensity on the third color. After these, I have included 6 colors which are also a mix of only two elemental colors but where one of the two mixed colors is half intensity, so you get the third class of colors including orange, yellow-green, violet, and sky blue.
To draw something on the grid, select a color and use the left mouse button to draw that color on the grid. What you are doing by drawing is setting that boid/cell to a fixed R, G, B color with 0 ease, meaning that it's color will not change or be affected by it's neighbors.
To Erase a drawn on cell, (or make it dynamic again), use the right mouse button.
The "Show" link shows the ease along with the color of each cell. Ease is represented visually as the opposite of black. So you will see black cells where there is very low ease. Likewise, higher-ease cells are seen more as the color which represents the RGB point of that cell. This way, ease looks like an extra texture over the current color grid, where color moves slower through darker cells.
The "3D View" is a direct boids view of the current grid. It shows the same exact data, but as positions in orthogonal 3D space. (color of each cell is included so you can identify which boid represents which grid cell). Click on it again to change back to normal grid view.
Theory
Technically the boids algorithm is n-Dimensional; each boid can be on a point in any number of dimensions. For my purposes, I only added one more dimension. Each boid has a parameter for R, G, B and E. E is the ease of the velocity vector. So technically the ease parameter affects all other parameters just as time is linked to motion in space. If the ease parameter (E) is somewhere near 1, the R,G,B vector for the given boid would be what it actually is. In the 2D grid view, it would appear that red, green, and blue pass through this boid with normal velocity. If E goes below 1, the 3D velocity vector scales down and any passing (R,G,B) wave appears to pass through that boid slower than normal, and likewise for values higher than 1. Ease affects the vector along r, g, and b dimensions equally, or said for a global scope, red, green and blue waves propagate through the grid at an equal velocity given by the ease vector of each cell. Higher spatial systems could also be included in the future which could include grouping
I placed a maximum limit on the Ease parameter for each boid system-wide, but technically each boid can have an E anywhere between 0 and easeMax. The result is a more turbulent wave-front when a wave propagates from an emitter.
You could call the colored cells you place on the grid emmitters, or looking at the whole thing another way you could call it a standing 4-Dimensional wave. In this case, the standing wave affects the waves around it, causing a gaussian effect. In yet another metaphorical way to look at this simulation, you could say that each cell in the grid is a 4 dimensional oscillator.
It is possible to change the overall maximum Ease such that color waves propagate through the grid space at higher or lower frequencies.
As color theory goes, light is expressed as hue; a looped spectrum based on placing the color red at each end of the spectrum. Beyond hue, there is also saturation (grey shift), and intensity (scaling from 0 to 1), commonly referred to as hue, saturation, lightness (HSL). RGB space and HSL space are two different shapes if the spectrum were to be modeled. Both shapes are 3D, but HSL space would be represented as a cylinder whereas RGB space is a cube. A point in RGB space correlates directly to a point in HSL space. But a line between a pair of correlating points in each space would traverse a differnent "path" of colors. The middle point of the spaces is the color we refer to as grey. RGB space is how computer monitors emulate HSL space, hence why most programmers are used to thinking of colors as RGB.
In my findings playing with the simulations, I saw that if the space is initialized with "random" color (I use the term random very loosely), each elemental color propagates in waves through the space seemingly without interacting with each other. This is logical because if a color is 100% red (r=255), then the entire brightness of color has already been used, and green and blue cannot exist in that same grid point because they have no room left in the color space to move (they are in the extrem red corner of the cube).
If, instead of random initialization, the space is initialized with grey (R,G,B balanced on the center point), upon drawing a colored emitter, it's complementary color begins to propagate at the wavefront of that color. So if you draw a red cell, a cyan emerges from the system and vice versa. The same goes for the green/magenta and blue/yellow complementary pairs. It seems that because of the complementary wave pattern caused by the waves themselves, and the fact that grey is the first color in the grid, the complementary color can only exist wherever the emitter's color does not exist. It is to say that not only is there no "red", but that there is technically "negative red" caused by systemic equilibrium. The secondary colors to me, in this system seem a lot like a correlation to electromagnetic waves or other combinatorial waves where the wavefront is completely synchronized between the two types of energy.. until you through a Blue emitter on the grid ;), then all cyan waves deconstruct into de-coupled blue and green wavefronts.
Looking further into this phenomenon, I realized it was becauese of a hyperparameter of ease propagation which I just called "easeEase". easeEase is a global variable which controls the step value of ease in each velocity vector of each cell. It is to say that if Ease has become a dimension (represented as a parameter in each cell, just like R, G, and B) instead of being a set hyperparameter, there is a new hyperparameter which must control how quickly Ease itself adjusts it's own vector. To put it another way, easeEase is the equivalent of the acceleration of time, system-wide. Based on this value, all colors waves will propagate through the grid at higher or lower velocities relative to the local ease vector of each cell. In future versions of WaveGrid I want to experiment with the idea of making easeEase a dimension and creating a new hyperparameter for easeEaseEase! Technically this process could go on forever, generating larger and more complicated emergent patterns.
To play with "time acceleration" change the "ease max" value, putting a speed limit on ease/velocity/wave frequency and propagation.
Try drawing different shapes and seeing how waves get trapped inside of them.
One thing I noticed when using "Show" ease feature was that when you draw a color on just one cell, the first iterations of ease are very predictable 4-fold geometric shapes which emanate from the center point, but at a certain size, classical chaos takes over and the pattern which you see becomes very unpredictable.
Changing the ease maximum limit really generates some interesting behaviors in the system. Since easeEase is set at 0.8, easeMax at certain factors of this generates some visible patterns in which specific cells light up with a certain color, and then slowly dissapate back into another color, a sort of grid of these points shows up at easeMax values between 0.15 and 0.367. Around easeMax=0.367, the pattern of supercharged cells becomes very sparse and sporadic, often times cells just briefly touching some color at very high velocity and then bouncing back quckly to another color, and generating a wave that propagates through the grid space. This is a general effect of making ease a dimension. At easeMax values higher than 1, a weird "droplet wave" effect can be seen in the grid. It looks like water droplets in a pond, generating large circular waves which interfere with each other. At easeMax > 2, you start to get into some very unpredictable behavior and hyperpatterns begin to form like large fluctuating arbitrary color boundary spaces which move and absorb each other. If you let easeMax=20 run for awhile, you can see these shapes emerge.
Annealing Example Video
You can do what I call "annealing" which is like turning easeMax up to 20, then turning it back down after so many frames to 0.05. The whole screen flickers for a time that is proportionate to however long you let it run at easeMax=20, the whole time cleaning out the super-cells to just their hulls, and then the large flickering super-cells anneal, smallest first, filling in with a sort of quadratic gaussian gradient depending on the color "energy" available in the space. If you look at the space after all of the waves "slow down" their filling of the cavities, you will notice that waves propagating through the space are all slowed down in a very weird way. If you then try to draw a color emitter anywhere in grid space, it will seem that the color wave is very tightly confined to the emitter, but the fluctuations in color around the emitter show a very high frame rate. I'm still trying to figure this effect out, but it's really fun to play with.

This next one is a larger grid space, (4x larger, but slower to render)... where I just placed one white emitter in roughly the center of the space, then did the annealing trick after the wave grew to an "interesting enough" size inside of the grey area... (placed white emitter: easeMax=1, changed easeMax to 20, waited a bit until cavities formed, changed easeMax back down to 0.05 and waited for annealing effect)
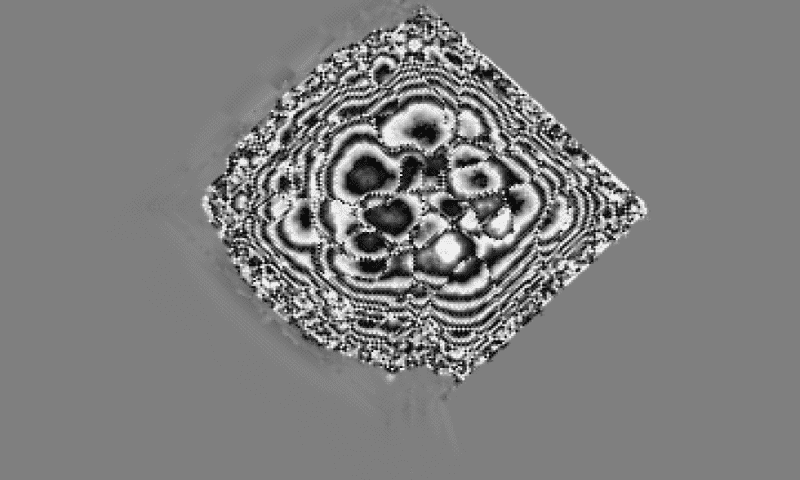
This is the same one, but many iterations later... some interesting super-slow moving waves propagate into the grey space. Side note: using only greyscale is like these waves only propagating on a plane in 3D position space.
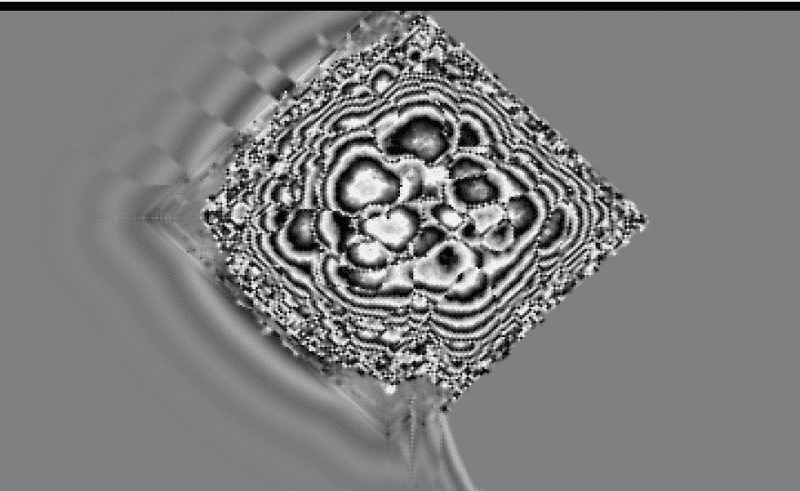
I made this post, because I was done playing with this thing myself and decided to share. Maybe you guys can see it has some sort of actual use in studying multidimensional wave propagation through a matrix of diferentially linked oscillators, or some other such thing. I love all of the interpretation value of it when it comes to quantum mechanics, specifically matrix mechanics. It's a very different way of looking at wave propagation and boundary equations, generating the same answer from a completely different point of view.
One question I have is, if the observational matrix (grid) became 3D, how would the third dimension be extrapolated, and depending on how it's done, how would that effect the final outcome. So far it's been countless hours of fun to modify and play with this concept, thinking about physics and reality the entire time.
Here's the simulator link again.
Follow the link below to play with my experimental sandbox. The rest of this post includes some instructions for use and then observations and a little bit of theory.
WaveGrid Demo - play with the simulator here, but read at least enough of what's below to understand it ;)
I took an open source art project written by someone else and turned it into a simulator of a 4D dynamical system, which you can "paint" on. Original code can be found on rectangleworld here
The part I liked about the original project is that the guy represented a 3D boids simulation using the actual "local neighborhood" as a continuous 2D grid through which the cells are arranged visually like cellular automata. One emergent feature I saw in rendering boids like this was that you could actually observe a wave-like behavior in the 2D grid, since the 3D location was represented as an (R,G,B) color. So it's structure is (X,Y,Z) = (GridX, GridY, (R, G, B))
Most people when trying to visualize the boids algorithm use just the plain x,y,z coordinates... and in order to make the algorithm more "true-to-form", they attempt to use a partitioning algorithm (like kdTree) in order to find a local neighborhood on each frame. The default alternative was to generate a pre-calculated local neighborhood as was the case with the original manifestation of the algorithm. So the author simply took this apparent error and turned it into an advantage.
In the Algorithm, each individual boid is linked to it's 8 surrounding neighbors upon initialization forming a lattice by which they share their location point in each dimension as well as their n-dimensional velocity vector. Technically each boid on each frame "observes" it's neighbors and uses that observational data to recalculate it's own velocity vector, which is in turn, observed by each of it's neighbors (a . The great part about the Grid (or the observational matrix) is that through the grid you can see how the different colors interact with each other. Using this method, higher than 3 dimensions can be represented visually through a 2D grid. The other advantage is that technically two boids can occupy the same exact point in 3D space without reacting to each other, which when extrapolated to the 2D view, means that two cells can be the same exact color, which, when using partitioning, is not possible.Usage
The grid starts out with all boids being "Grey" with 0 ease {r: 127, g: 127, b: 127, e: 0}. The 4D velocity vector of each boid is set to 0.
Along the bottom of the view, you have colors, as well as a global ease setting and a couple of other options. The colors are set up in a way that black,white is one group, then the elemental colors R, G, and B. After that are the mixed colors like cyan, magenta and yellow. These colors are secondary colors to the R,G,B space because they include a mix of maximum intensity of two colors and 0 intensity on the third color. After these, I have included 6 colors which are also a mix of only two elemental colors but where one of the two mixed colors is half intensity, so you get the third class of colors including orange, yellow-green, violet, and sky blue.
To draw something on the grid, select a color and use the left mouse button to draw that color on the grid. What you are doing by drawing is setting that boid/cell to a fixed R, G, B color with 0 ease, meaning that it's color will not change or be affected by it's neighbors.
To Erase a drawn on cell, (or make it dynamic again), use the right mouse button.
The "Show" link shows the ease along with the color of each cell. Ease is represented visually as the opposite of black. So you will see black cells where there is very low ease. Likewise, higher-ease cells are seen more as the color which represents the RGB point of that cell. This way, ease looks like an extra texture over the current color grid, where color moves slower through darker cells.
The "3D View" is a direct boids view of the current grid. It shows the same exact data, but as positions in orthogonal 3D space. (color of each cell is included so you can identify which boid represents which grid cell). Click on it again to change back to normal grid view.
Theory
Technically the boids algorithm is n-Dimensional; each boid can be on a point in any number of dimensions. For my purposes, I only added one more dimension. Each boid has a parameter for R, G, B and E. E is the ease of the velocity vector. So technically the ease parameter affects all other parameters just as time is linked to motion in space. If the ease parameter (E) is somewhere near 1, the R,G,B vector for the given boid would be what it actually is. In the 2D grid view, it would appear that red, green, and blue pass through this boid with normal velocity. If E goes below 1, the 3D velocity vector scales down and any passing (R,G,B) wave appears to pass through that boid slower than normal, and likewise for values higher than 1. Ease affects the vector along r, g, and b dimensions equally, or said for a global scope, red, green and blue waves propagate through the grid at an equal velocity given by the ease vector of each cell. Higher spatial systems could also be included in the future which could include grouping
I placed a maximum limit on the Ease parameter for each boid system-wide, but technically each boid can have an E anywhere between 0 and easeMax. The result is a more turbulent wave-front when a wave propagates from an emitter.
You could call the colored cells you place on the grid emmitters, or looking at the whole thing another way you could call it a standing 4-Dimensional wave. In this case, the standing wave affects the waves around it, causing a gaussian effect. In yet another metaphorical way to look at this simulation, you could say that each cell in the grid is a 4 dimensional oscillator.
It is possible to change the overall maximum Ease such that color waves propagate through the grid space at higher or lower frequencies.
As color theory goes, light is expressed as hue; a looped spectrum based on placing the color red at each end of the spectrum. Beyond hue, there is also saturation (grey shift), and intensity (scaling from 0 to 1), commonly referred to as hue, saturation, lightness (HSL). RGB space and HSL space are two different shapes if the spectrum were to be modeled. Both shapes are 3D, but HSL space would be represented as a cylinder whereas RGB space is a cube. A point in RGB space correlates directly to a point in HSL space. But a line between a pair of correlating points in each space would traverse a differnent "path" of colors. The middle point of the spaces is the color we refer to as grey. RGB space is how computer monitors emulate HSL space, hence why most programmers are used to thinking of colors as RGB.
In my findings playing with the simulations, I saw that if the space is initialized with "random" color (I use the term random very loosely), each elemental color propagates in waves through the space seemingly without interacting with each other. This is logical because if a color is 100% red (r=255), then the entire brightness of color has already been used, and green and blue cannot exist in that same grid point because they have no room left in the color space to move (they are in the extrem red corner of the cube).
If, instead of random initialization, the space is initialized with grey (R,G,B balanced on the center point), upon drawing a colored emitter, it's complementary color begins to propagate at the wavefront of that color. So if you draw a red cell, a cyan emerges from the system and vice versa. The same goes for the green/magenta and blue/yellow complementary pairs. It seems that because of the complementary wave pattern caused by the waves themselves, and the fact that grey is the first color in the grid, the complementary color can only exist wherever the emitter's color does not exist. It is to say that not only is there no "red", but that there is technically "negative red" caused by systemic equilibrium. The secondary colors to me, in this system seem a lot like a correlation to electromagnetic waves or other combinatorial waves where the wavefront is completely synchronized between the two types of energy.. until you through a Blue emitter on the grid ;), then all cyan waves deconstruct into de-coupled blue and green wavefronts.
Looking further into this phenomenon, I realized it was becauese of a hyperparameter of ease propagation which I just called "easeEase". easeEase is a global variable which controls the step value of ease in each velocity vector of each cell. It is to say that if Ease has become a dimension (represented as a parameter in each cell, just like R, G, and B) instead of being a set hyperparameter, there is a new hyperparameter which must control how quickly Ease itself adjusts it's own vector. To put it another way, easeEase is the equivalent of the acceleration of time, system-wide. Based on this value, all colors waves will propagate through the grid at higher or lower velocities relative to the local ease vector of each cell. In future versions of WaveGrid I want to experiment with the idea of making easeEase a dimension and creating a new hyperparameter for easeEaseEase! Technically this process could go on forever, generating larger and more complicated emergent patterns.
To play with "time acceleration" change the "ease max" value, putting a speed limit on ease/velocity/wave frequency and propagation.
Try drawing different shapes and seeing how waves get trapped inside of them.
One thing I noticed when using "Show" ease feature was that when you draw a color on just one cell, the first iterations of ease are very predictable 4-fold geometric shapes which emanate from the center point, but at a certain size, classical chaos takes over and the pattern which you see becomes very unpredictable.
Changing the ease maximum limit really generates some interesting behaviors in the system. Since easeEase is set at 0.8, easeMax at certain factors of this generates some visible patterns in which specific cells light up with a certain color, and then slowly dissapate back into another color, a sort of grid of these points shows up at easeMax values between 0.15 and 0.367. Around easeMax=0.367, the pattern of supercharged cells becomes very sparse and sporadic, often times cells just briefly touching some color at very high velocity and then bouncing back quckly to another color, and generating a wave that propagates through the grid space. This is a general effect of making ease a dimension. At easeMax values higher than 1, a weird "droplet wave" effect can be seen in the grid. It looks like water droplets in a pond, generating large circular waves which interfere with each other. At easeMax > 2, you start to get into some very unpredictable behavior and hyperpatterns begin to form like large fluctuating arbitrary color boundary spaces which move and absorb each other. If you let easeMax=20 run for awhile, you can see these shapes emerge.
Annealing Example Video
You can do what I call "annealing" which is like turning easeMax up to 20, then turning it back down after so many frames to 0.05. The whole screen flickers for a time that is proportionate to however long you let it run at easeMax=20, the whole time cleaning out the super-cells to just their hulls, and then the large flickering super-cells anneal, smallest first, filling in with a sort of quadratic gaussian gradient depending on the color "energy" available in the space. If you look at the space after all of the waves "slow down" their filling of the cavities, you will notice that waves propagating through the space are all slowed down in a very weird way. If you then try to draw a color emitter anywhere in grid space, it will seem that the color wave is very tightly confined to the emitter, but the fluctuations in color around the emitter show a very high frame rate. I'm still trying to figure this effect out, but it's really fun to play with.
This next one is a larger grid space, (4x larger, but slower to render)... where I just placed one white emitter in roughly the center of the space, then did the annealing trick after the wave grew to an "interesting enough" size inside of the grey area... (placed white emitter: easeMax=1, changed easeMax to 20, waited a bit until cavities formed, changed easeMax back down to 0.05 and waited for annealing effect)
This is the same one, but many iterations later... some interesting super-slow moving waves propagate into the grey space. Side note: using only greyscale is like these waves only propagating on a plane in 3D position space.
I made this post, because I was done playing with this thing myself and decided to share. Maybe you guys can see it has some sort of actual use in studying multidimensional wave propagation through a matrix of diferentially linked oscillators, or some other such thing. I love all of the interpretation value of it when it comes to quantum mechanics, specifically matrix mechanics. It's a very different way of looking at wave propagation and boundary equations, generating the same answer from a completely different point of view.
One question I have is, if the observational matrix (grid) became 3D, how would the third dimension be extrapolated, and depending on how it's done, how would that effect the final outcome. So far it's been countless hours of fun to modify and play with this concept, thinking about physics and reality the entire time.
Here's the simulator link again.
Attachments
Last edited by a moderator: