How fast is this bead traveling down the wire

[Ronaldo21]

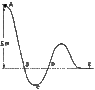
A big metal bead slides due to gravity along an upright frictiion-free wire. It starts from rest at the top of the wire as shown in the sketch. How fast is it traveling as it passes.

http://https://www.physicsforums.com/attachment.php?attachmentid=22509&stc=1&d=1260854052

Point B?
Point D?
Point E?
At what point does it have the maximum speed?
I got B for this because it goes down really fast.

 

[AEM]

The way to do this question is to use conservation of energy.

Gravitational PE at top goes into PE + KE as the bead slides down.

 

[Ronaldo21]

so what do we exactly do?
because we don't have the number to d and e. i think i get b.

 

[AEM]

so what do we exactly do?
because we don't have the number to d and e. i think i get b.

I think you might want to review the concept of conservation of energy for objects falling in a gravitational field. Briefly, you pick a reference level where potential energy = 0. When the object is above that level its PE is given by mgx where x is its current height. The conservation of energy equation goes as

Energy at the start = mgx + \frac{1}{2} m v^2

Here your energy at the start is mgh. Now look at your drawing carefully. Where IS the object going the fastest? This is subtle because it's where the PE is the LEAST. What is the relationship between points b, d, e? Which one is highest? Or they all at the same height?

 

[Ronaldo21]

hmm i think i get it so the answer will be some kind of formula then right??

 

[AEM]

hmm i think i get it so the answer will be some kind of formula then right??

Actually you can get a numerical answer for the speed at points b, d, e if you pick your reference level (PE = 0, x = 0) along the horizontal line passing through b, d, e. You cannot get a numerical answer for point c because you don't know how far below point b it is.