How is this array of capacitors connected: Serie or parallel?

[sergioro]

Homework Statement

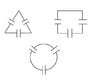
The figure shows three capacitors with capacitances C₁, C₂, and C₃. How are they connected: in parallel or in series?


|------| |------|
|.....| (middle dots don't mean any thing. they help keep lines in place)
|---| |---| |---|

Homework Equations

Serie connection: 1/c = 1/c₁+ 1/c₂+1/c₃ ...
parallel: c= c₁+ c₂+c₃ ...

The Attempt at a Solution

I would say that anyone of the capacitors is in parallel with the other two who are in serie. I can get this by making a rotation (either counterclockwise or clockwise) of the capacitors one by one so I can always get the same configuration shown in the figure
(one on top and two in the bottom).

How can I prove it using equations.

Sergio

 

[cepheid]

|------| |------|
|               |    
|---| |---| |---|

If this is indeed the situation, then it's obvious just by inspection that one of the caps is in parallel with the series combo of the other two. I'm not sure what you mean by "prove it using equations." If you want to figure out how the caps are connected to each other, you do that by looking at them.

 

[sergio_123]

Thanks cepheid.

That's the array of caps (how did you make the white spaces in between the vertical lines?).

What is causing trouble is the following:
Call c₁ and c₂ the caps on bottom and c₃ the one on top.

Let's say c₂ is charged elsewhere and then inserted in the circuit in
its position at the bottom.

Following the figure, c₁ will get the same charge as c₂ (they are in serie) and c₃ will get something else. This means that if one take the circuit appart each cap will have the computed amount of charge.

Now, If one view the same circuit in a different way, say that is c₁ who is in parallel with c₂ and c₃, then c₃ will have the same charge of c₂ and c₁ will get something else. This means that if one take the circuit apart the distribution of charges is interchanged between c₁ and c₃.

This does not look right to me. It seems as if the physical process depends on the labeling.

Sergio

 

[CWatters]

Consider these circuits which are identical to yours. The question "which capacitors are in series/parallel" can't be answered because the circuit is ambiguous (edit: Perhaps ambiguous is the wrong word). If you add the words "between these two nodes" then it can be answered.

Depending on which two nodes you choose the following are correct answers:

(C1+C2)//C3
(C2+C3)//C1
(C3+C1)//C2

where I'm using
+ = Series
// = parallel

To an engineer your version of the circuit implies you are talking about the two vertical nodes (one on the left and right).

If the capacitors are all the same value then all three answers give same result.

 

[NascentOxygen]

Let's say c₂ is charged elsewhere and then inserted in the circuit in
its position at the bottom.

Following the figure, c₁ will get the same charge as c₂ (they are in serie) and c₃ will get something else.

You changed your ID?

Capacitors in series get the same charge only if they are in series while being charged. If they are charged separately and then connected in series, their final charges are unlikely going to be equal. (Though what you can say is that any charge C1 loses will be matched by C2 losing the same, if they are in series while being discharged.)