Homework Help Overview
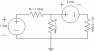
The discussion revolves around understanding how to assign currents in a DC circuit, particularly when analyzing circuits with batteries and resistors. The original poster expresses confusion about the number of currents to define based on the circuit's components and structure.
Discussion Character
- Exploratory, Assumption checking
Approaches and Questions Raised
- Participants discuss the process of defining currents in circuits, with some suggesting that each component should have at least one current associated with it. Questions arise about how to determine the number of currents needed based on the circuit's configuration.
Discussion Status
Some participants have provided guidance on using current loops and emphasized the importance of ensuring that each component is associated with a current. There are multiple interpretations of how to approach the problem, and the discussion is ongoing without a clear consensus.
Contextual Notes
The original poster notes that there could be different currents through each battery or resistor unless they are in series, which adds to the complexity of defining currents in the circuit.